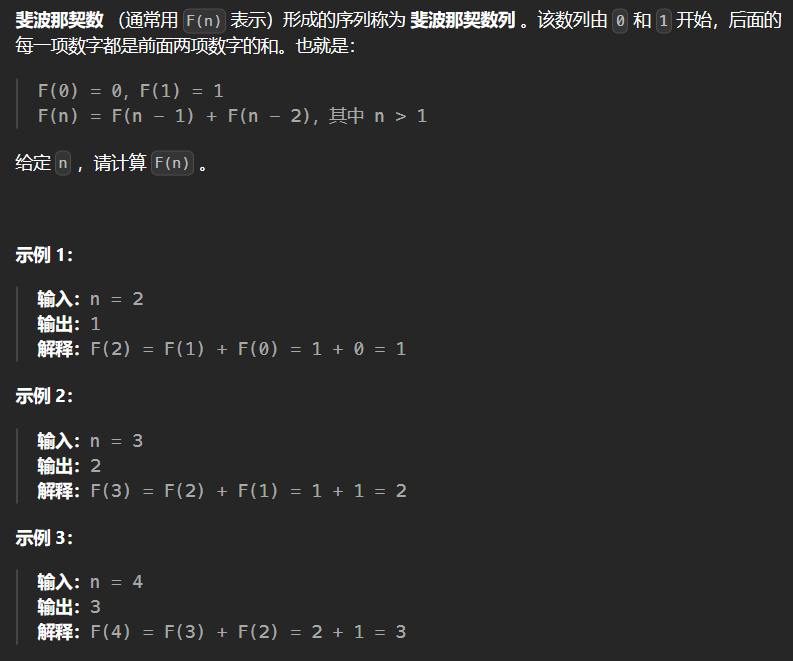
1. 基础题目

1.1 509-斐波那契数

509

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int fib(int n) {
        if(n <= 1)
            return n;
        int dp[2];
        dp[0] = 0;
        dp[1] = 1;
        int sum;
        for(int i = 2; i <= n; ++i)
        {
            sum = dp[0]+dp[1];
            dp[0] = dp[1];
            dp[1] = sum;
        }
        return sum;
    }
};

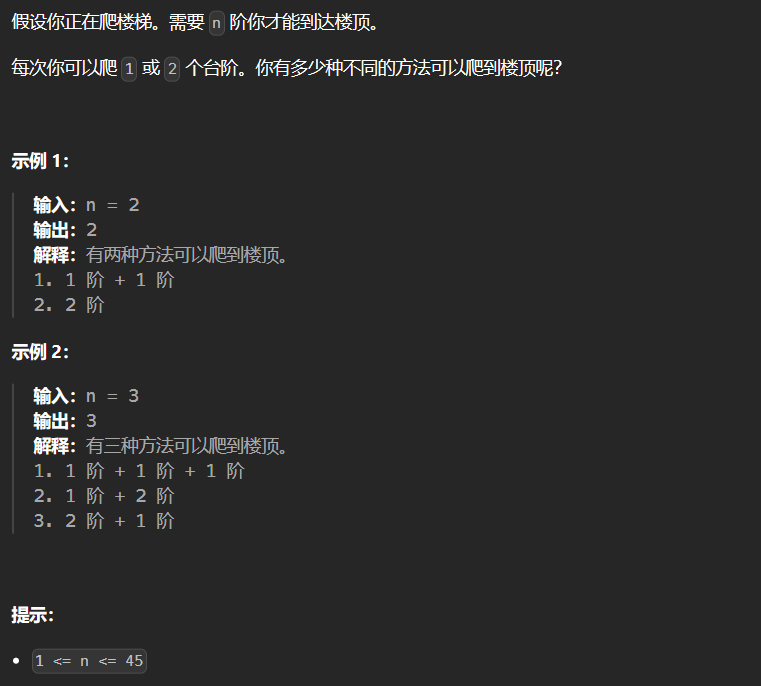
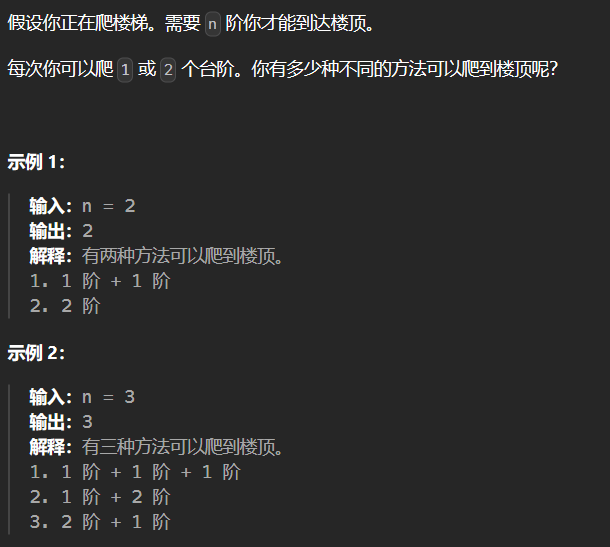
1.2 70-爬楼梯

70

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int climbStairs(int n) {
        if(n<=2)
            return n;
        int dp[3];
        dp[1] = 1;
        dp[2] = 2;
        int sum;
        for(int i = 3; i <= n; ++i)
        {
            sum = dp[1] + dp[2];
            dp[1] = dp[2];
            dp[2] = sum;
        }
        return sum;
    }
};

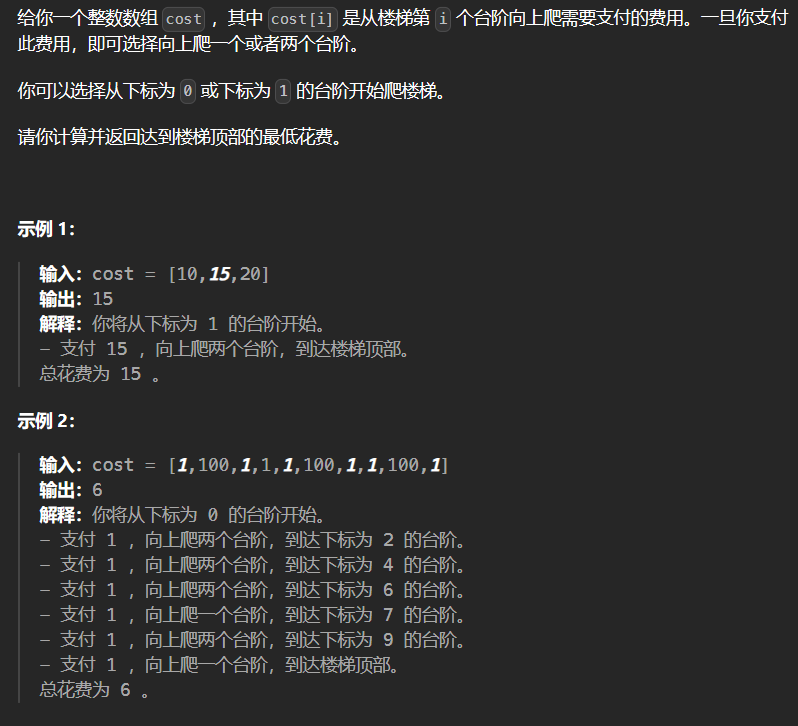
1.3 746-使用最小花费爬楼梯

746

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        int dp0 = 0;
        int dp1 = 0;
        int dpi;
        for(int i = 2; i <= cost.size(); ++i)
        {
            dpi = min(cost[i-1]+dp1,cost[i-2]+dp0);
            dp0 = dp1;
            dp1 = dpi;
        }
        return dpi;
    }
};

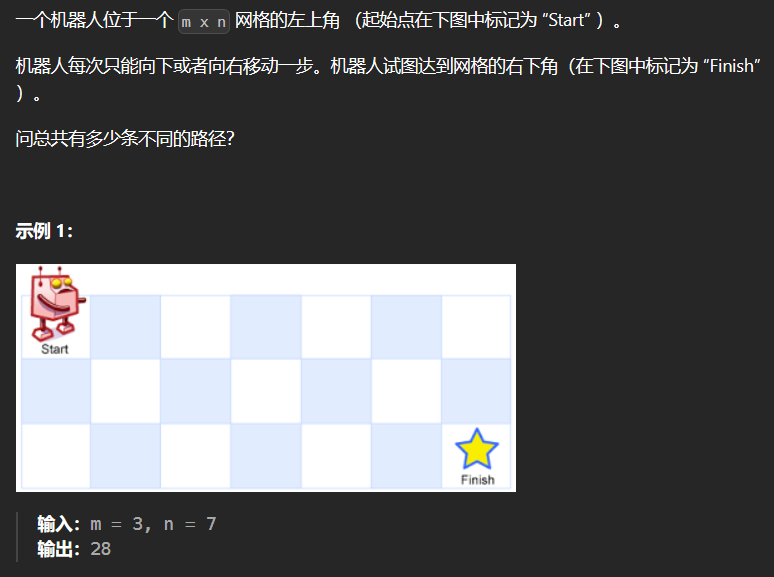
1.4 62-不同路径

62

便于理解的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int uniquePaths(int m, int n) {
        //dp[i][j] 到达i,j坐标处的路径数
        //dp[i][j] = dp[i-1][j] + dp[i][j-1];
        vector<vector<int>> dp(m,vector<int>(n));
        for(int i = 0; i < m; ++i)
            dp[i][0] = 1;
        for(int j = 0; j < n; ++j)
            dp[0][j] = 1;

        for(int i = 1; i < m; ++i)
        {
            for(int j = 1; j < n; ++j)
            {
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
};

以上方法时间空间复杂度都为O(MN)
用滚动数组代替上面这种方式(效率一样,空间复杂度降低为O(N))

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<int> f(n,1);
        for (int i = 1; i < m; ++i)  //将上面的方式累加到一行中
            for (int j = 1; j < n; ++j) 
                f[j]+=f[j-1];

        return f[n - 1];
    }
};

还有组合数方法, 暂且不提,其时间复杂度可以达到O(M),空间复杂度为O(1)

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    int uniquePaths(int m, int n) {
        long long ans = 1;
        for (int x = n, y = 1; y < m; ++x, ++y) {
            ans = ans * x / y;
        }
        return ans;
    }
};

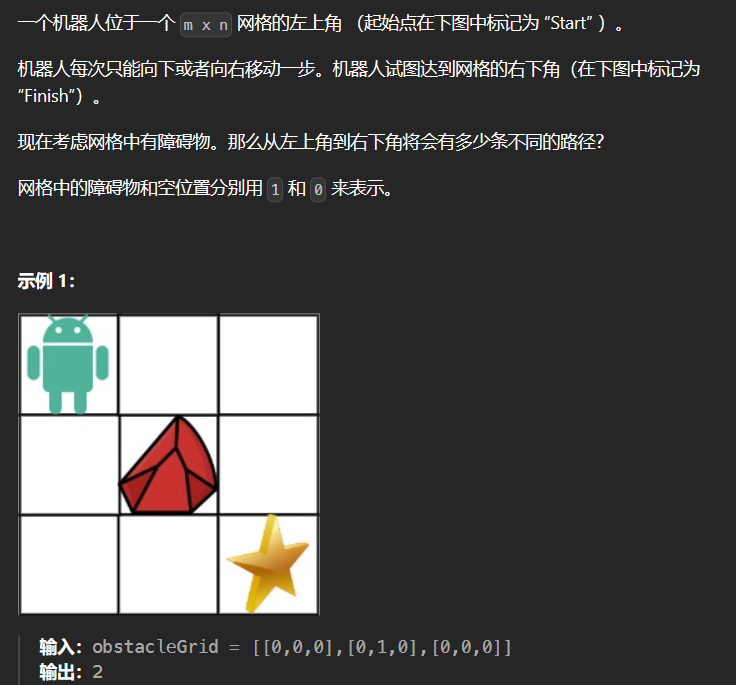
1.5 63-不同路径II

63

时间空间复杂度都为O(MN)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m = obstacleGrid.size();
        int n = obstacleGrid.at(0).size();
        if(obstacleGrid[m-1][n-1] == 1 || obstacleGrid[0][0] == 1) //起终点有障碍
            return 0;
        vector<vector<int>> dp(m,vector<int>(n,0)); //初始化为0,以便忽略障碍物
        for(int i = 0; i < m && obstacleGrid[i][0] == 0; ++i) //初始化列
            dp[i][0] = 1;
        for(int i = 0; i < n && obstacleGrid[0][i] == 0; ++i) //初始化行
            dp[0][i] = 1;
        for(int i = 1; i < m; ++i)
            for(int j = 1; j < n; ++j)
                if(obstacleGrid[i][j] != 1) //有障碍直接忽略
                    dp[i][j] = dp[i-1][j] + dp[i][j-1];
        return dp[m-1][n-1];
    }
};

空间复杂度减少至O(M)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int n = obstacleGrid.size();
        int m = obstacleGrid.at(0).size();
        vector <int> dp(m);

        dp[0] = (obstacleGrid[0][0] == 0);
        for (int i = 0; i < n; ++i) 
        {
            for (int j = 0; j < m; ++j) 
            {
                if (obstacleGrid[i][j] == 1) 
                    dp[j] = 0;
                else if(j - 1 >= 0 && obstacleGrid[i][j - 1] == 0) 
                    dp[j] += dp[j - 1];
            }
        }
        return dp.back();
    }
};

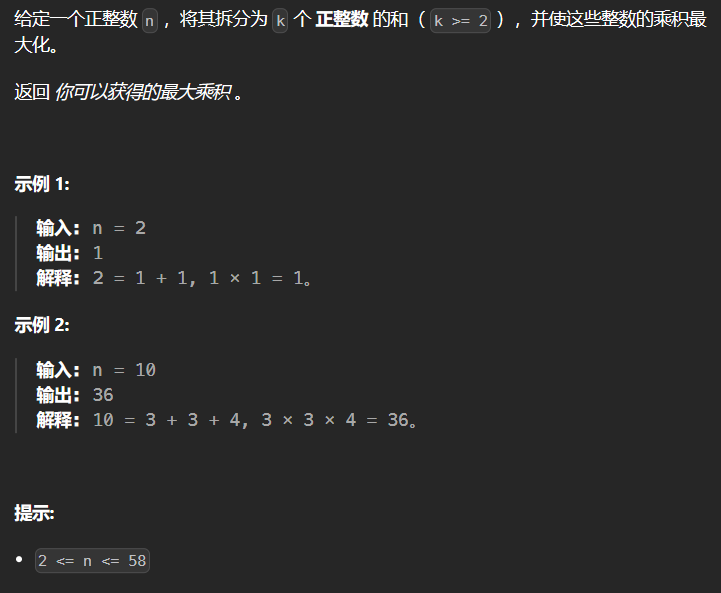
1.6 343-整数拆分

343

时间复杂度为O(n^2)
空间复杂度为O(n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int integerBreak(int n) {
        vector<int> dp(n+1);
        for(int i = 2; i <= n; ++i) //算n前面的数,以推断出n的最大积
        {
            int curmax = 0; 
            for(int j = 1; j < i; ++j) //拆分为两个数和多个数进行大小比较
                curmax = max(curmax, max(j * (i-j) , j * dp[i-j]) );
            dp[i] = curmax;
        }
        return dp[n];
    }
};

利用数学知识可以将时间空间复杂度都降低至O(1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int integerBreak(int n) {
        if (n <= 3) 
            return n - 1;
        int quotient = n / 3;
        int remainder = n % 3;
        if (remainder == 0) 
            return (int)pow(3, quotient);
        else if (remainder == 1)
            return (int)pow(3, quotient - 1) * 4;
        else
            return (int)pow(3, quotient) * 2;
    }
};

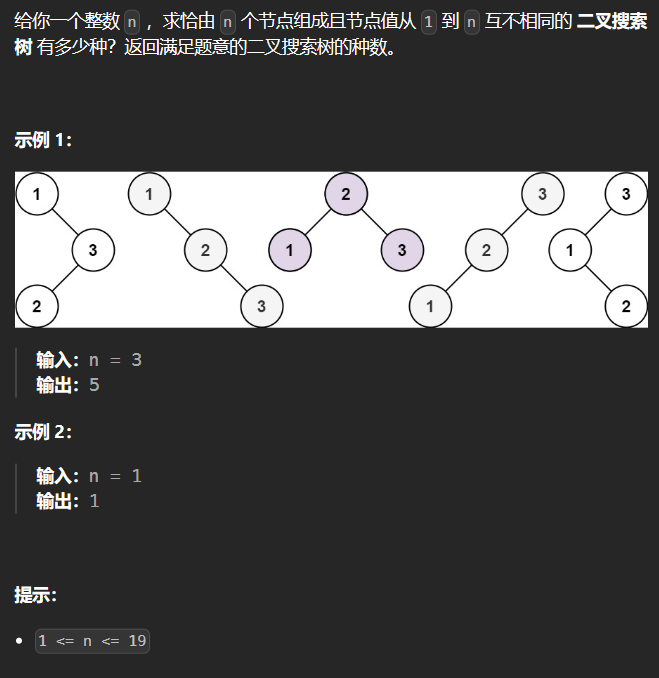
1.7 96-不同的二叉搜索树

96

最简单的方式仍然需要进行公式的推导
并且时间复杂度有O(N^2)
空间复杂度O(N)

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int numTrees(int n) {
        vector<int> dp(n+1,0);
        dp[0] = 1; //空树也可以看作是一个搜索二叉树
        dp[1] = 1;

        for(int i = 2; i <= n; ++i)
            for(int j = 1; j <= i; ++j)
                dp[i] += dp[j-1] * dp[i-j]; //需要通过例子算出dp的推导过程
        return dp[n];
    }
};

进行数学运算,涉及到 卡塔兰数 ,可使时间复杂度达到O(N),空间复杂度达到O(1)

1
2
3
4
5
6
7
8
9
class Solution {
public:
    int numTrees(int n) {
        long long C = 1;
        for (int i = 0; i < n; ++i) 
            C = C * 2 * (2 * i + 1) / (i + 2);
        return (int)C;
    }
};

2. 背包问题

2.1 背包问题基础

二维dp实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <bits/stdc++.h>
using namespace std;

int n,bagweight; //bagweight是最大携带重量

void solve()
{
    vector<int> weight(n,0); //物品所占重量
    vector<int> value(n,0); //物品价值
    for(int i = 0; i < n; ++i)
        cin >> weight[i];
    for(int i = 0; i < n; ++i)
        cin>>value[i];
    
    
    //dp数组
    vector<vector<int>> dp(weight.size(),vector<int>(bagweight+1,0));
    for(int i = weight[0]; i <= bagweight; ++i)
        dp[0][i] = value[0];
    
    for(int i = 1; i < weight.size();++i)
        for(int j = 0; j <= bagweight; ++j)
        {
            if(j < weight[i]) //装不下就继承上一次的价值
                dp[i][j] = dp[i-1][j];
            else
                dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);
        }
    
    cout<<dp[weight.size()-1][bagweight] << endl;
}

int main()
{
    while(cin >> n >>bagweight)
        solve();
    return 0;
}

一维dp实现(滚动数组)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
// 一维dp数组实现
#include <iostream>
#include <vector>
using namespace std;

int main() 
{
    // 读取 M 和 N
    int M, N;
    cin >> M >> N;

    vector<int> costs(M);
    vector<int> values(M);

    for (int i = 0; i < M; i++)
        cin >> costs[i];
    for (int j = 0; j < M; j++)
        cin >> values[j];

    // 创建一个动态规划数组dp，初始值为0
    vector<int> dp(N + 1, 0);

    // 外层循环遍历每个类型的研究材料
    for (int i = 0; i < M; ++i)
        // 内层循环从 N 空间逐渐减少到当前研究材料所占空间
        for (int j = N; j >= costs[i]; --j)
            // 考虑当前研究材料选择和不选择的情况，选择最大值
            dp[j] = max(dp[j], dp[j - costs[i]] + values[i]);
    // 输出dp[N]，即在给定 N 行李空间可以携带的研究材料最大价值
    cout << dp[N] << endl;
    return 0;
}

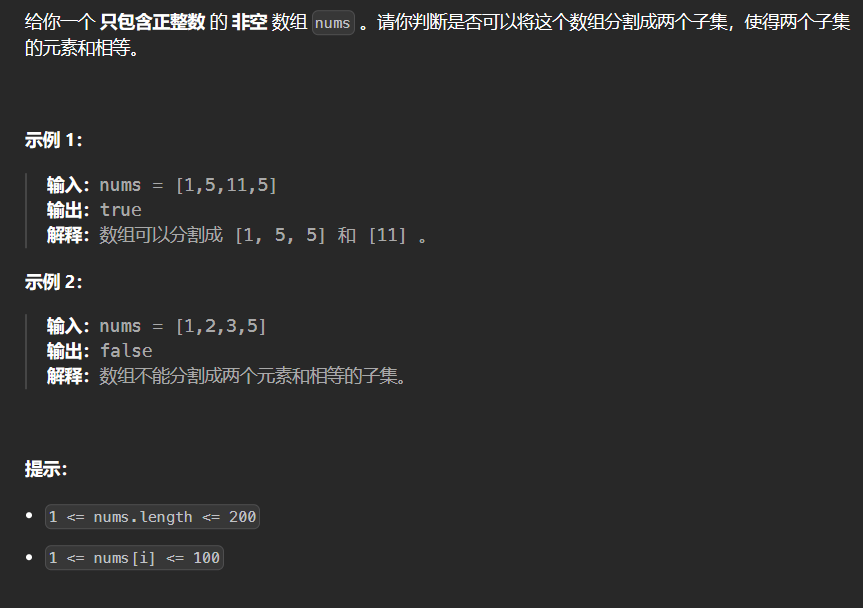
2.2 416-分割等和子集

416

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int sum = 0;
        for(auto e: nums)
            sum+=e;
        if(sum % 2 == 1) //判断能否分为两部分
            return false; 
        int target = sum/2; //目标

        vector<int> dp(10001,0); //dp[i]代表着i的空间最多放多少
        for(int i = 0; i < nums.size(); ++i)
            for(int j = target; j >= nums[i]; --j)
                dp[j] = max(dp[j],dp[j-nums[i]]+nums[i]);
        
        if(dp[target] == target)
            return true;
        return false;
    }
};

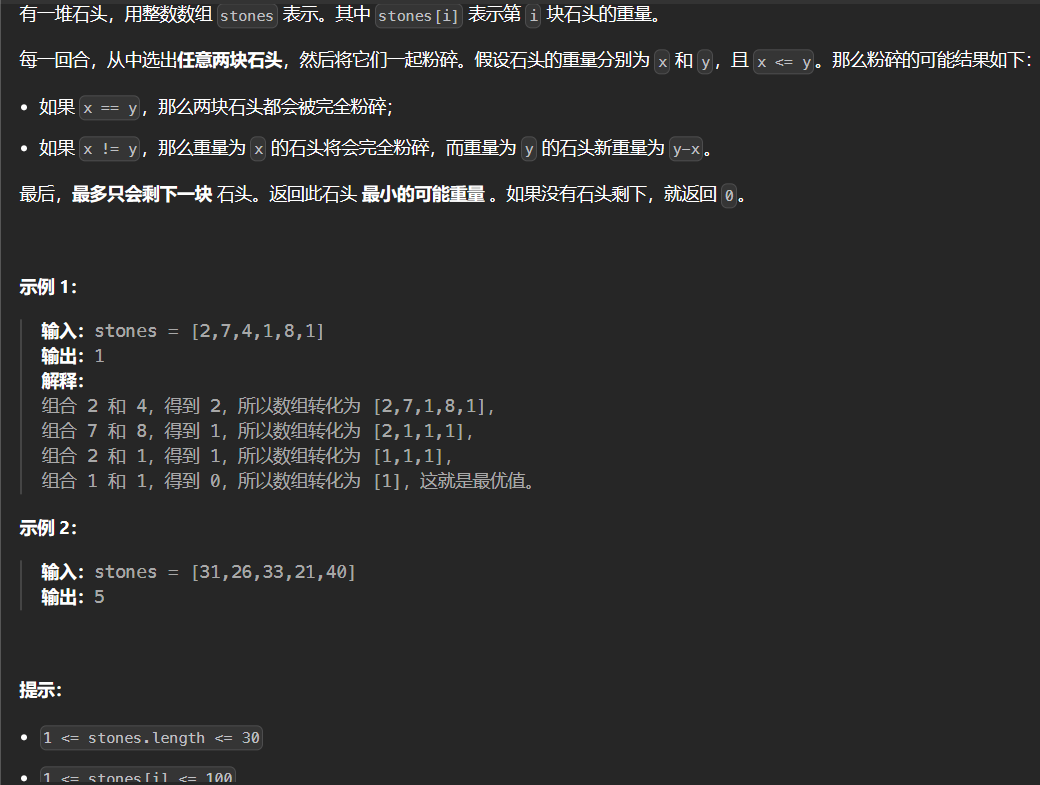
2.3 1049-最后一块石头的重量II

1049

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int lastStoneWeightII(vector<int>& stones) 
    {
        vector<int> dp(15001, 0);
        int sum = 0;
        for(auto e : stones)
            sum+=e;
        int target = sum / 2;

        for (int i = 0; i < stones.size(); i++)  // 遍历物品
            for (int j = target; j >= stones[i]; j--)  // 遍历背包
                dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
        //23 11
        return sum - dp[target] - dp[target];
    }
};

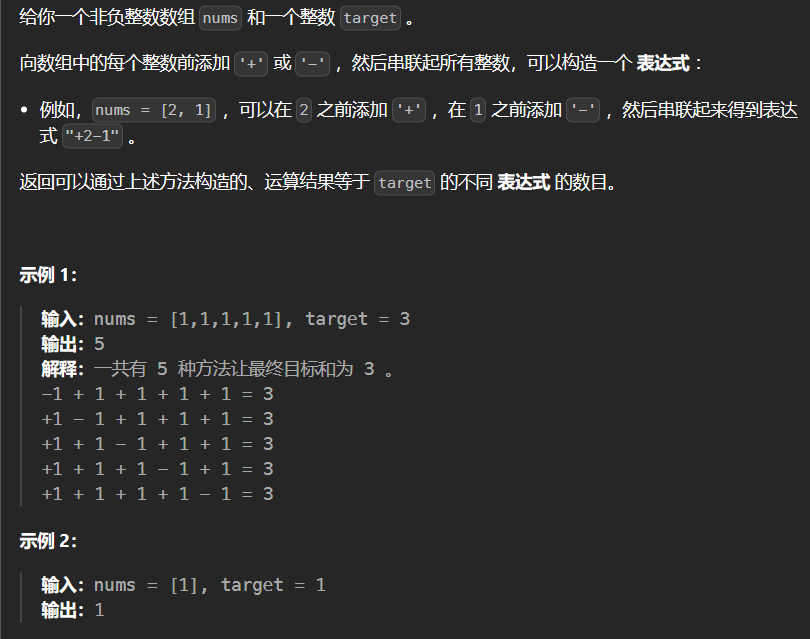
2.4 494-目标和

494

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        int sum = 0;
        for (auto e : nums) 
            sum += e;
        if (abs(target) > sum || (target + sum) % 2 == 1) 
            return 0; // 此时没有方案

        int bagSize = (target + sum) / 2;
        vector<int> dp(bagSize + 1, 0);
        dp[0] = 1;
        for (int i = 0; i < nums.size(); i++) 
            for (int j = bagSize; j >= nums[i]; j--) 
                dp[j] += dp[j - nums[i]];
        return dp[bagSize];
    }
};

2.5 474-一和零

474

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        vector<vector<int>> dp(m + 1, vector<int> (n + 1, 0)); // 默认初始化0
        for (string str : strs) 
        { // 遍历物品
            int oneNum = 0, zeroNum = 0;
            for (char c : str) 
            {
                if (c == '0')   
                    zeroNum++;
                else 
                    oneNum++;
            }
            for (int i = m; i >= zeroNum; i--)  // 遍历背包容量且从后向前遍历！
                for (int j = n; j >= oneNum; j--)
                    dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
        }
        return dp[m][n];
    }
};

完全背包问题:

2.6 518-零钱兑换II

518

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int change(int amount, vector<int>& coins) {
        vector<int> dp(amount+1,0);
        dp[0] = 1;

        for(int i = 0; i < coins.size(); ++i)
            for(int j = coins[i]; j <= amount; ++j)
                dp[j] += dp[j-coins[i]];
        return dp[amount];
    }
};

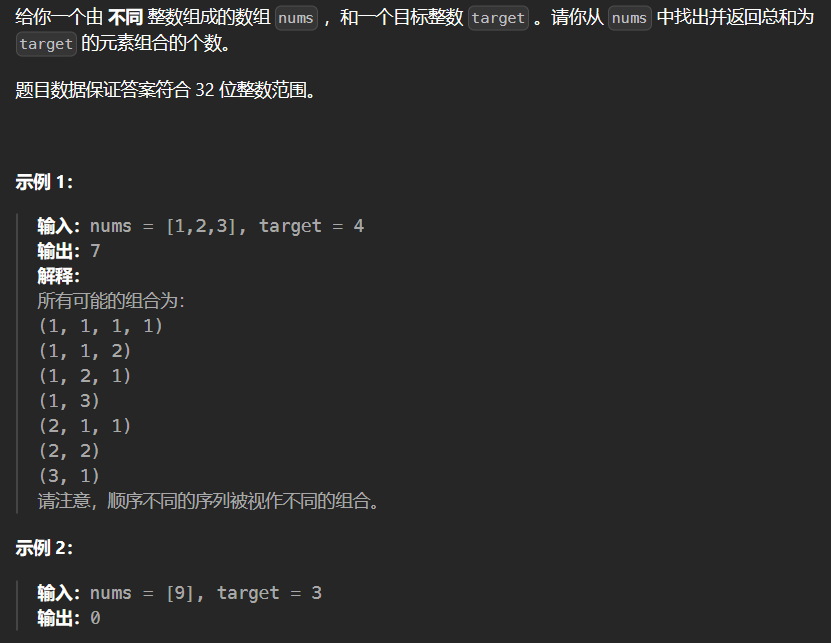
2.7 377-组合综合IV

377

和上一题的区别在于这是组合,即(1,3)和(3,1)可看为两组

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int combinationSum4(vector<int>& nums, int target) {
        vector<int> dp(target + 1, 0);
        dp[0] = 1;
        for (int i = 0; i <= target; i++) //遍历背包
            for (int j = 0; j < nums.size(); j++) 
                if (i >= nums[j] && dp[i] < INT_MAX - dp[i - nums[j]]) 
                    dp[i] += dp[i - nums[j]];
        return dp[target];
    }
};

2.8 70-爬楼梯

70

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int climbStairs(int n) {
        vector<int> dp(n+1,0);
        dp[0] = 1;

        for(int i = 1; i <= n; ++i)
            for(int j = 1; j <= 2; ++j)
                if(i>=j)
                    dp[i] += dp[i-j];
        return dp[n];
    }
};

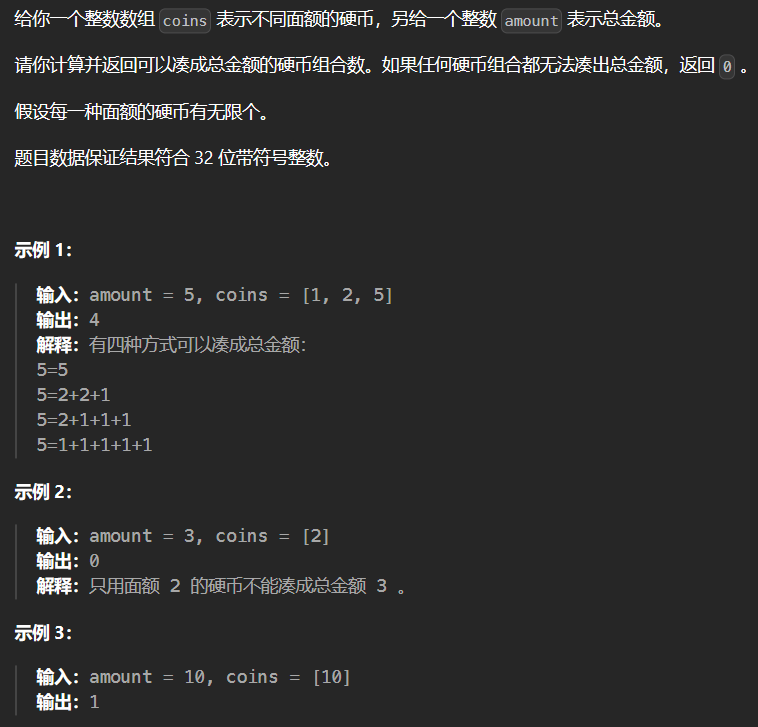
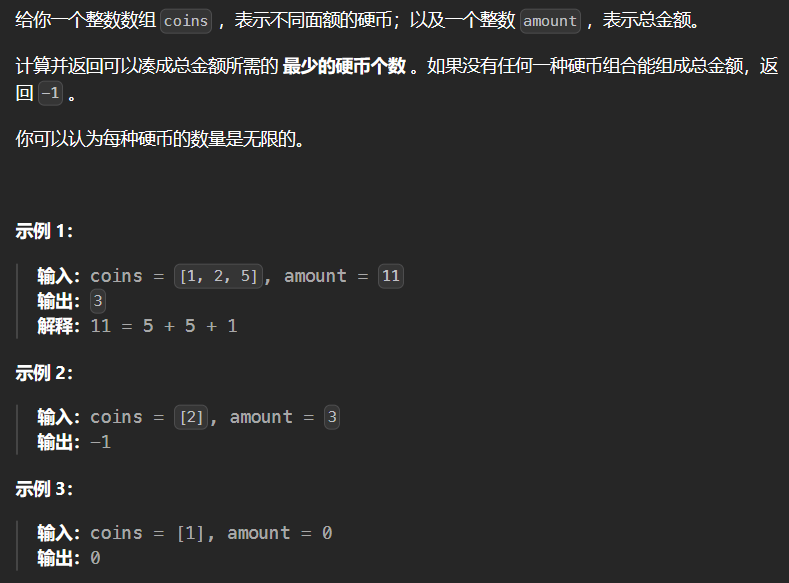
2.9 322-零钱兑换

322

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        vector<int> dp(amount+1,INT_MAX);
        dp[0] = 0;

        for(int i = 1; i <= amount; ++i)
            for(int j = 0; j < coins.size(); ++j)
                if(i >= coins[j] && dp[i-coins[j]] != INT_MAX)
                    dp[i] = min(dp[i-coins[j]]+1,dp[i]);
        if(dp[amount] == INT_MAX)
            return -1;
        return dp[amount];
    }
};

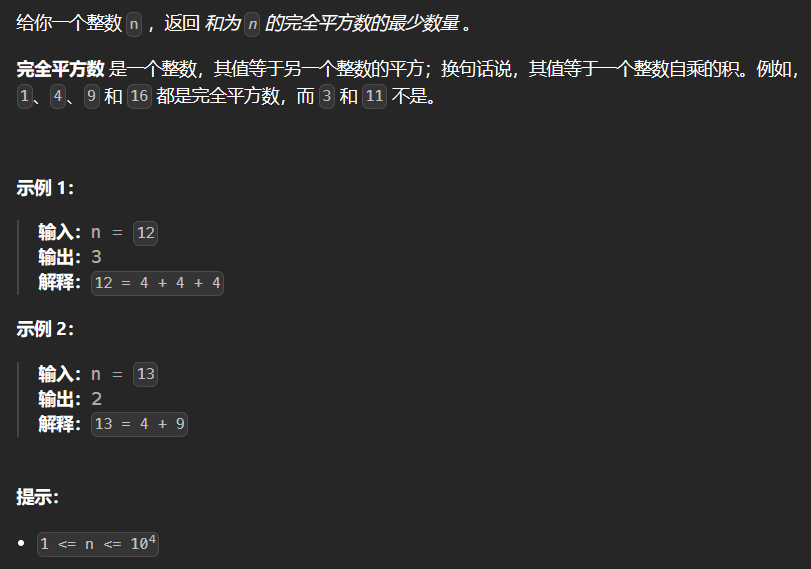
2.10 279-完全平方数

279

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int numSquares(int n) {
        vector<int> dp(n+1,INT_MAX);
        dp[0] = 0;

        for(int i = 0; i <= n; ++i)
            for(int j = 1; j*j <= i; ++j)
                dp[i] = min(dp[i],dp[i-j*j]+1);
        return dp[n];
    }
};

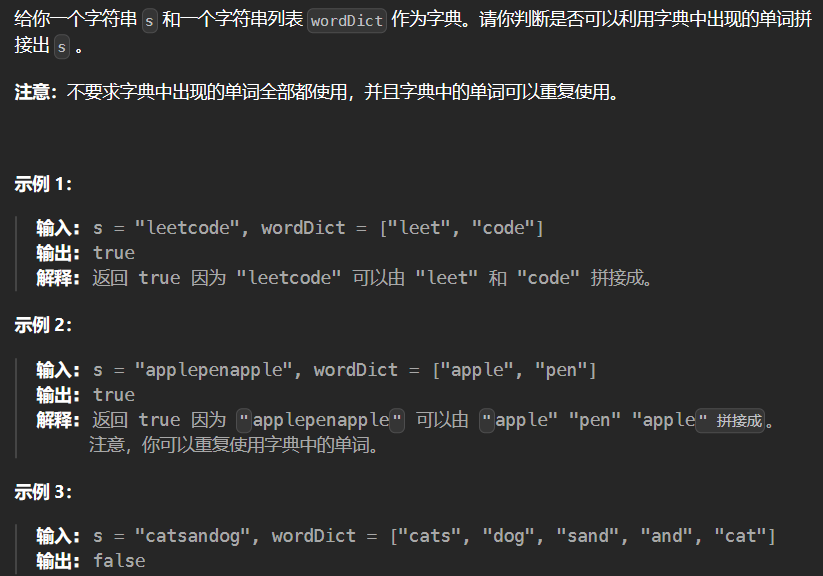
2.11 239-单词拆分

139

难

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        unordered_set<string> wordSet(wordDict.begin(),wordDict.end());
        vector<bool> dp(s.size()+1,false);
        dp[0] = true;

        for(int i = 1; i <= s.size(); ++i)
            for(int j = 0; j<i ;++j)
            {
                string word = s.substr(j,i-j);
                if(wordSet.find(word) != wordSet.end() && dp[j])
                    dp[i] = true;
            }
        return dp[s.size()];
    }
};

3. 打家劫舍问题

3.1 198-打家劫舍

198

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int rob(vector<int>& nums) {
        if(nums.size() == 0)
            return 0;
        if(nums.size() == 1)
            return nums[0];

        vector<int> dp(nums.size());
        dp[0] = nums[0];
        dp[1] = max(nums[0],nums[1]);
        for(int i = 2; i < nums.size(); ++i)
            dp[i] = max(dp[i-2]+nums[i],dp[i-1]);
        return dp[nums.size()-1];
    }
};

3.2 213-打家劫舍II

213

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int robrange(vector<int>& nums,int start,int end)
    {
        if(end == start)
            return nums[start];
        vector<int> dp(nums.size());

        dp[start] = nums[start];
        dp[start+1] = max(nums[start],nums[start+1]);

        for(int i = start+2; i <= end; ++i)
            dp[i] = max(dp[i-2]+nums[i],dp[i-1]);
        return dp[end];
    }
    int rob(vector<int>& nums) {
        if(nums.size() == 0)
            return 0;
        if(nums.size() == 1)
            return nums[0];
        int ans1 = robrange(nums,0,nums.size()-2); //不考虑尾
        int ans2 = robrange(nums,1,nums.size()-1); //不考虑头
        return max(ans1,ans2);
    }
};

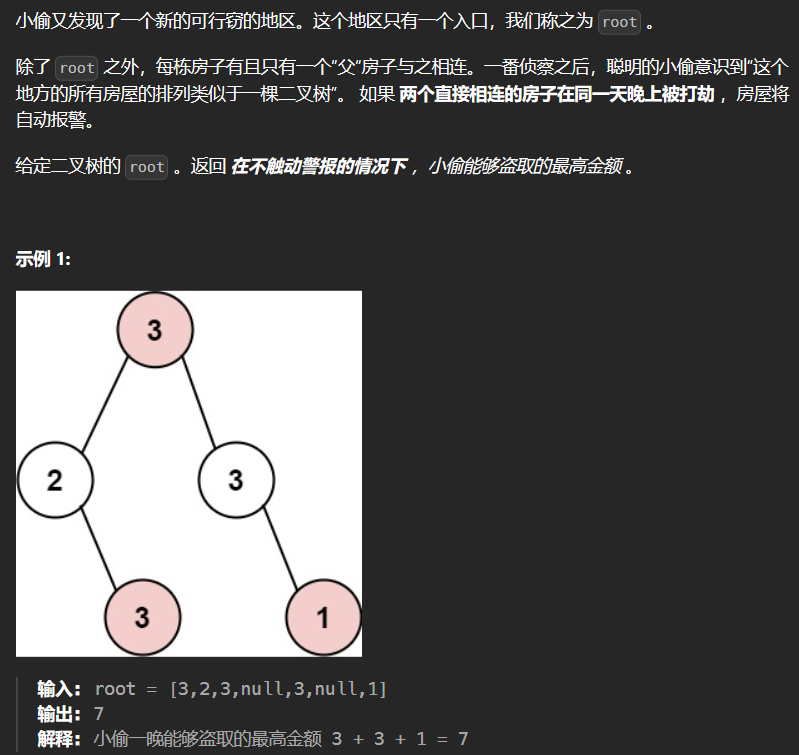
3.3 337-打家劫舍III

337

…

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    vector<int> robTree(TreeNode* cur)
    {
        if(!cur)
            return vector<int>{0,0};
        vector<int> left = robTree(cur->left);
        vector<int> right = robTree(cur->right);
        
        int val_cur = cur->val + left[0] + right[0];
        int val_nocur = max(left[0],left[1]) + max(right[0],right[1]);
        return {val_nocur,val_cur};
    }
    int rob(TreeNode* root) {
        vector<int> ans = robTree(root);
        return max(ans[0],ans[1]);
    }
};

4. 股票系列

4.1 121-买卖股票的最佳时机

121

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int size = prices.size();
        vector<vector<int>> dp(2,vector<int>(2)); //只开辟了2*2的大小
        dp[0][0] = -prices[0]; //买股票后的钱
        dp[0][1] = 0;          //卖股票后的钱
        for(int i = 1; i < size; ++i)
        {
            //买之前的和买现在的
            dp[i%2][0] = max(dp[(i-1)%2][0],-prices[i]);

            //之前卖出,和现在卖出取赚的最多的
            dp[i%2][1] = max(dp[(i-1)%2][1],prices[i] + dp[(i-1)%2][0]);
        }
        return dp[(size-1)%2][1];
    }
};

4.2 122-买卖股票的最佳时机II

122

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int size = prices.size();
        vector<vector<int>> dp(size,vector<int>(2,0));
        dp[0][0] = -prices[0];
        for(int i = 1; i < size; ++i)
        {
            //昨天不卖继续等和卖再买的价格对比取最大值
            dp[i][0] = max(dp[i-1][0],dp[i-1][1] - prices[i]);
            //昨天持有的最多钱对比今天买出去后持有的钱
            dp[i][1] = max(dp[i-1][1],dp[i-1][0] + prices[i]);
        }
        return dp[size-1][1];
    }
};

4.3* 123-买卖股票的最佳时机III

123

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int size = prices.size();
        if(size == 0)
            return 0;
        vector<int> dp(5,0);
        dp[1] = -prices[0];
        dp[3] = -prices[0];
        for(int i = 1; i < size; ++i)
        {
            dp[1] = max(dp[1],dp[0] - prices[i]);
            dp[2] = max(dp[2],dp[1] + prices[i]);
            dp[3] = max(dp[3],dp[2] - prices[i]);
            dp[4] = max(dp[4],dp[3] + prices[i]);
        }
        return dp[4];
    }
};

4.4* 188-买卖股票的最佳时机IV

188

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        int size = prices.size();
        vector<int> dp(k*2+1);
        for(int i = 1; i <= k; ++i)
            dp[i*2-1] = -prices[0];

        for(int i = 1; i < size; ++i)
        {
            for(int j = 1; j <= k*2-1; j+=2)
            {
                dp[j] = max(dp[j],dp[j-1] - prices[i]);
                dp[j+1] = max(dp[j+1],dp[j] + prices[i]);
            }
        }
        return dp[k*2];
    }
};

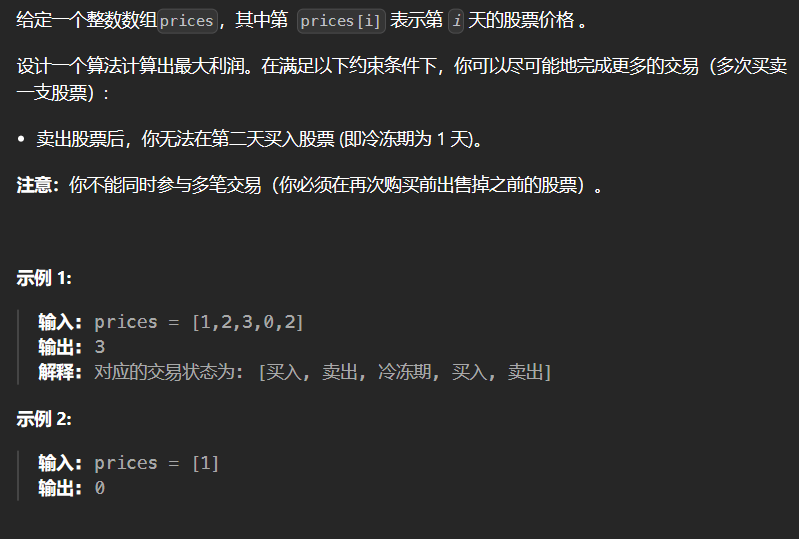
4.5 309-买卖股票的最佳时机含冷冻期

309

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int size = prices.size();
        vector<vector<int>> dp(size,vector<int>(4,0));
        //四种状态, 买入股票,卖出股票后度过冷冻期,今天刚卖出股票,冷冻期状态
        dp[0][0] -= prices[0];

        for(int i = 1; i < size; ++i)
        {
            //一直持有股票 对比 冷冻期后买入与今天买入股票的最大值
            dp[i][0] = max(dp[i-1][0],max(dp[i-1][3],dp[i-1][1]) - prices[i]);

            //前一天卖出股票和前一天是冷冻期
            dp[i][1] = max(dp[i-1][1],dp[i-1][3]);

            //正常卖出股票后的钱
            dp[i][2] = dp[i-1][0] + prices[i];

            //冷冻期
            dp[i][3] = dp[i-1][2];
            cout << dp[i][0] << " " << dp[i][1] << " " << dp[i][2] << " " << dp[i][3] << endl;
        }
        return max(dp[size-1][3],max(dp[size-1][1],dp[size-1][2]));
    }
};

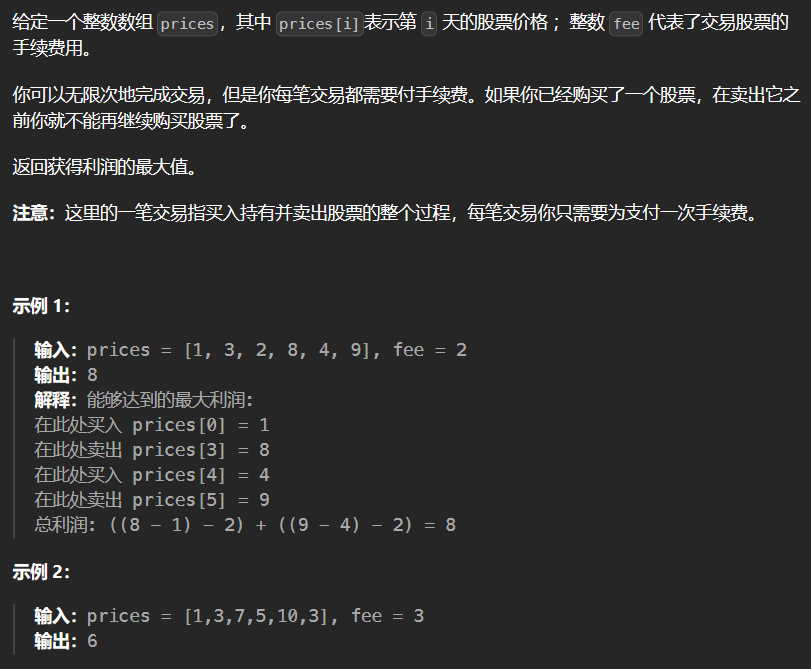
4.6 714-买卖股票的最佳时机含手续费

714

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        int size = prices.size();
        // vector<vector<int>> dp(size,vector<int>);
        vector<int> dp(2,0);
        dp[0] = -prices[0];

        for(int i = 1; i < size; ++i)
        {
            dp[0] = max(dp[0],dp[1] - prices[i]);
            dp[1] = max(dp[1],dp[0] + prices[i] - fee);
        }
        return max(dp[0],dp[1]);
    }
};

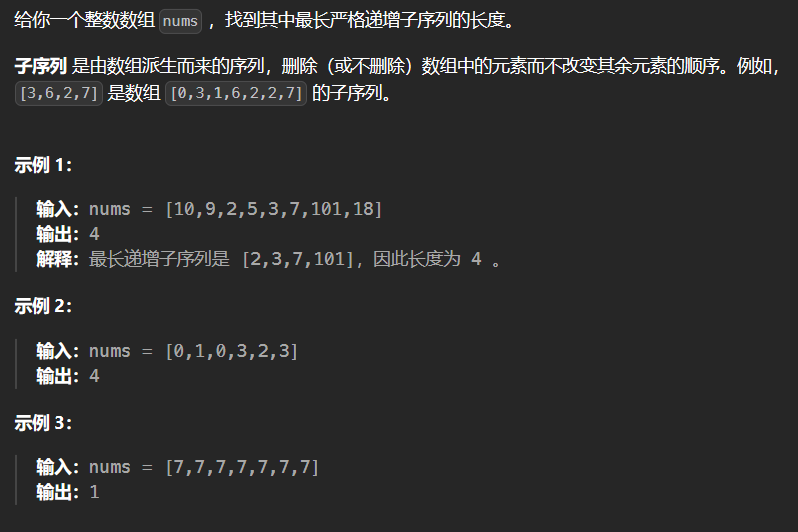
5. 子序列问题

5.1 300-最长递增子序列

300

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int size = nums.size();
        if(size == 1)
            return 1;
        vector<int> dp(size,1); //最小的递增子序列就是1,初始化为1
        int ans = 0;
        for(int i = 1; i < size; ++i)
        {
            for(int j = 0; j < i; ++j)
                if(nums[i] > nums[j]) //符合递增就+
                    dp[i] = max(dp[i],dp[j]+1);
            if(dp[i] > ans)
                ans = dp[i];
        }
        return ans;
    }
};

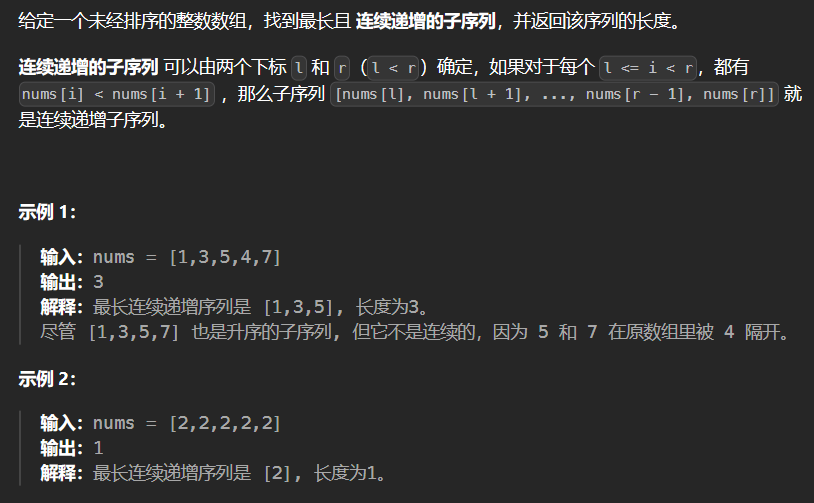
5.2 674-最长连续递增序列

674

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        int ans = 1;
        int size = nums.size();
        if(size == 1)
            return 1;
        vector<int> dp(size,1);
        for(int i = 1; i < size; ++i)
        {
            if(nums[i] > nums[i-1])
                dp[i] = max(dp[i-1]+1,dp[i-1]);
            if(dp[i] > ans)
                ans = dp[i];
        }
        return ans;
    }
};

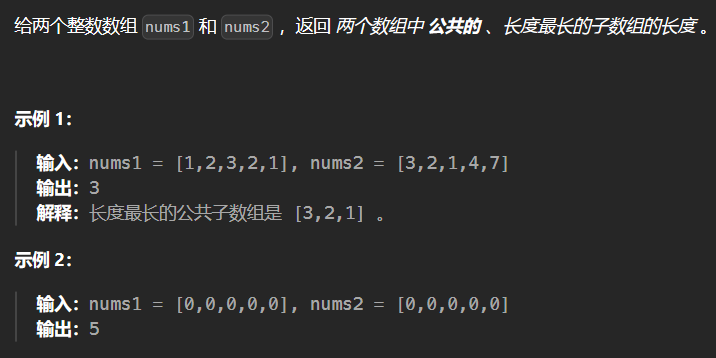
5.3 718-最长重复子数组

718

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        int size1 = nums1.size();
        int size2 = nums2.size();
        int ans = 0;
        vector<vector<int>> dp(size1+1,vector<int>(size2+1,0));
        for(int i = 1; i <= size1 ; ++i)
        {
            for(int j = 1; j <= size2; ++j)
            {
                if(nums1[i-1] == nums2[j-1])
                    dp[i][j] = dp[i-1][j-1]+1;
                if(dp[i][j] > ans)
                    ans = dp[i][j];
            }
        }
        return ans;
    }
};

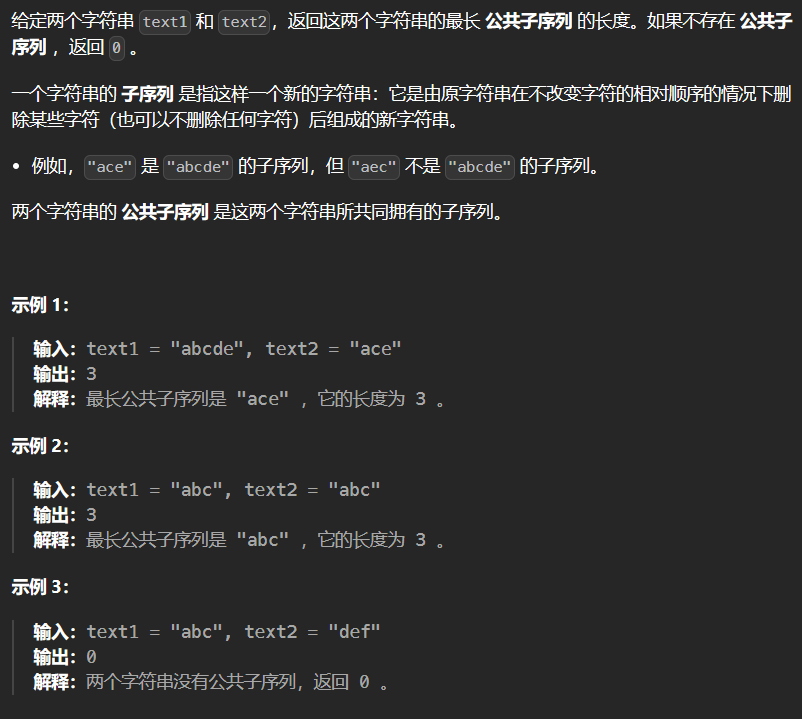
5.4 1143-最长公共子序列

1143

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int size1 = text1.size();
        int size2 = text2.size();
        int ans = 0;
        vector<vector<int>> dp(size1+1,vector<int>(size2+1));

        for(int i = 1; i <= size1; ++i)
        {
            for(int j = 1; j <= size2; ++j)
            {
                if(text1[i-1] == text2[j-1])
                    dp[i][j] = dp[i-1][j-1] + 1;
                else
                    dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
            }
        }
        return dp[size1][size2];
    }
};

5.5 1035-不相交的线

1035

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        int size1 = nums1.size();
        int size2 = nums2.size();
        vector<vector<int>> dp(size1+1,vector<int>(size2+1,0));

        for(int i = 1; i <= size1; ++i)
        {
            for(int j = 1; j <= size2; ++j)
            {
                if(nums1[i-1] == nums2[j-1])
                    dp[i][j] = dp[i-1][j-1] + 1;
                else
                    dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
            }
        }
        return dp[size1][size2];
    }
};

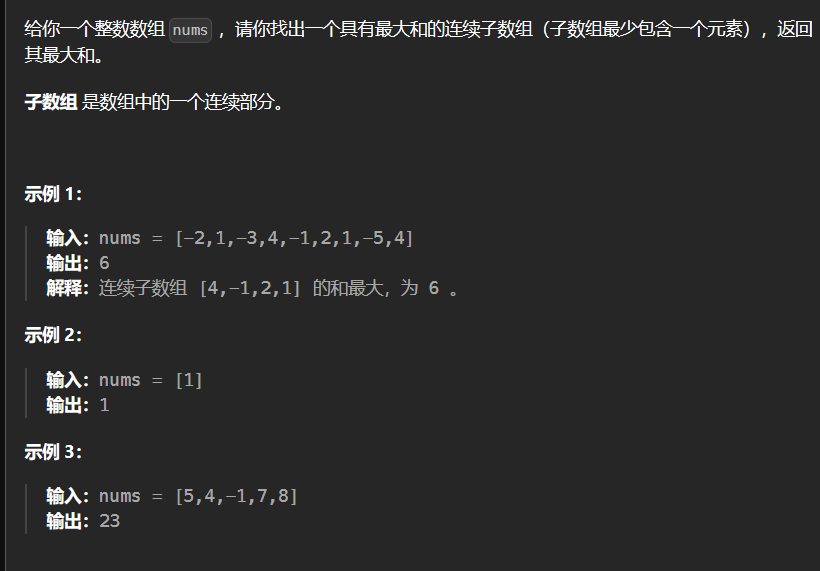
5.6 53-最大子数组和

53

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int size = nums.size();
        vector<int> dp(size,0);
        dp[0] = nums[0];
        int ans = dp[0];
        for(int i = 1; i < size; ++i)
        {
            dp[i] = max(dp[i-1]+nums[i],nums[i]);
            if(dp[i] > ans)
                ans = dp[i];
        }
        return ans;
    }
};

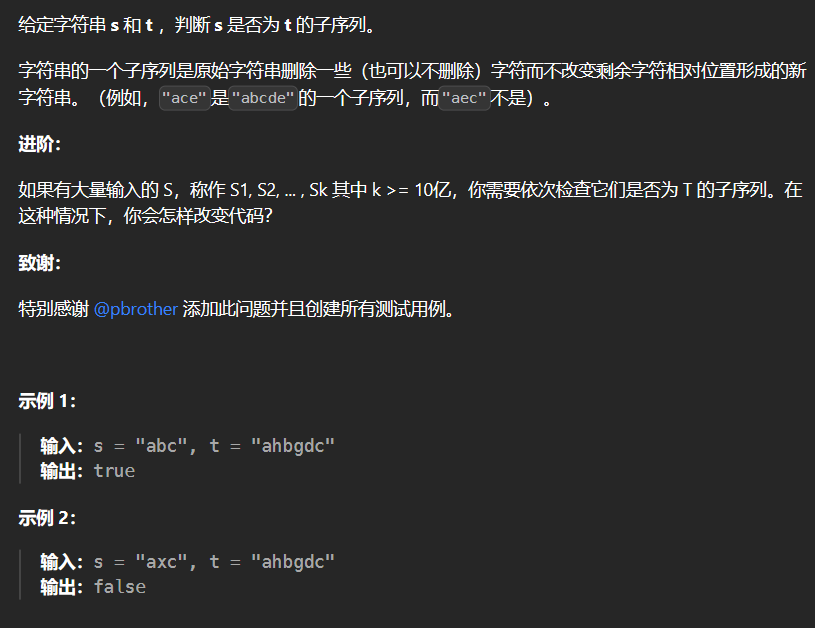
5.7 392-判断子序列

392

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    bool isSubsequence(string s, string t) {
        int size1 = s.size();
        int size2 = t.size();
        vector<vector<int>> dp(size1+1,vector<int>(size2+1,0));

        for(int i = 1; i <= size1; ++i)
        {
            for(int j = 1; j <= size2; ++j)
            {
                if(s[i-1] == t[j-1])
                    dp[i][j] = dp[i-1][j-1]+1;
                else
                    dp[i][j] = dp[i][j-1];
            }
        }
        if(dp[size1][size2] == size1)
            return true;
        return false;
    }
};

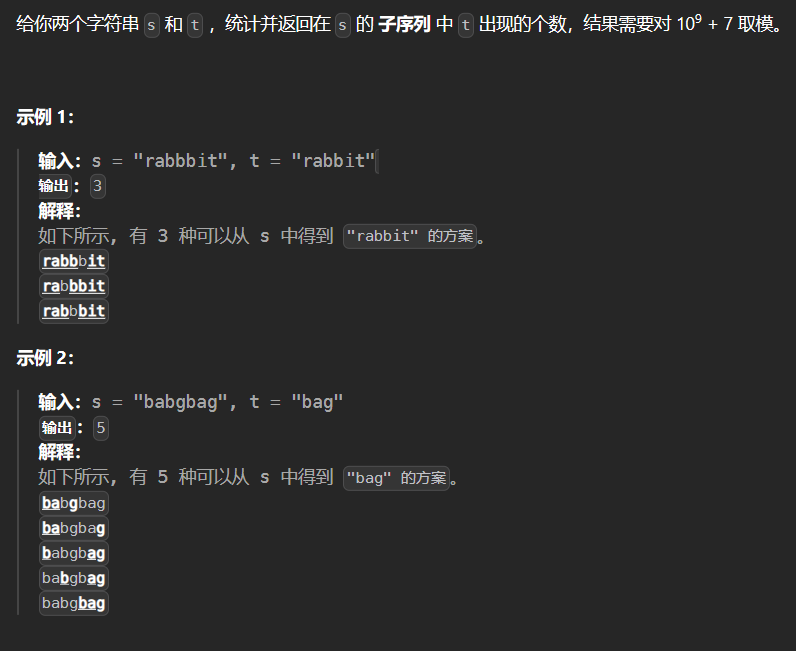
5.8* 115-不同的子序列

115

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int numDistinct(string s, string t) {
        int size1 = s.size();
        int size2 = t.size();
        vector<vector<uint64_t>> dp(size1+1,vector<uint64_t>(size2+1,0));
        for(int i = 0; i < size1; ++i)
            dp[i][0] = 1;
            
        for(int i = 1; i <= size1; ++i)
        {
            for(int j = 1; j <= size2; ++j)
            {
                if(s[i-1] == t[j-1])
                    dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
                else
                    dp[i][j] = dp[i-1][j];
            }
        }
        return dp[size1][size2];
    }
};

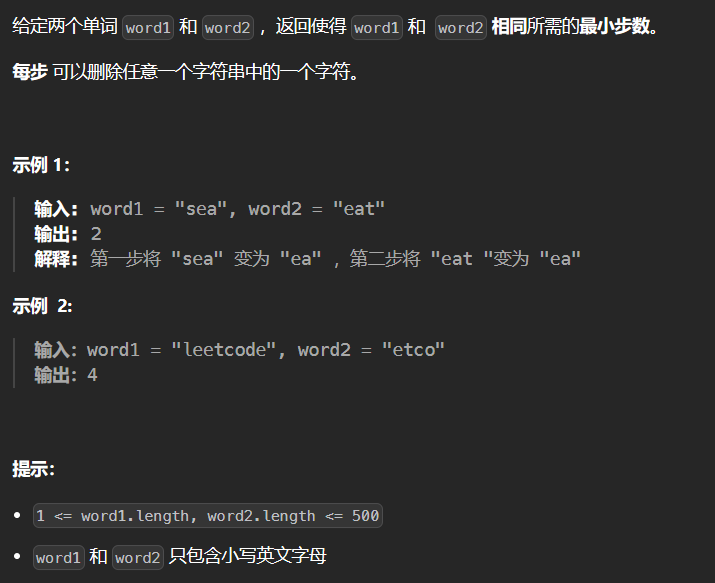
5.9 583-两个字符串的删除操作

583

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int minDistance(string word1, string word2) {
        int size1 = word1.size();
        int size2 = word2.size();
        vector<vector<int>> dp(size1+1,vector<int>(size2+1));
        for(int i = 0; i <= size1; ++i)
            dp[i][0] = i;
        for(int i = 0; i <= size2; ++i)
            dp[0][i] = i;
        
        for(int i = 1; i <= size1; ++i)
        {
            for(int j = 1; j <= size2; ++j)
            {
                if(word1[i-1] == word2[j-1])
                    dp[i][j] = dp[i-1][j-1];
                else
                    dp[i][j] = min(dp[i-1][j] + 1, dp[i][j-1] + 1);
            }
        }
        return dp[size1][size2];
    }
};

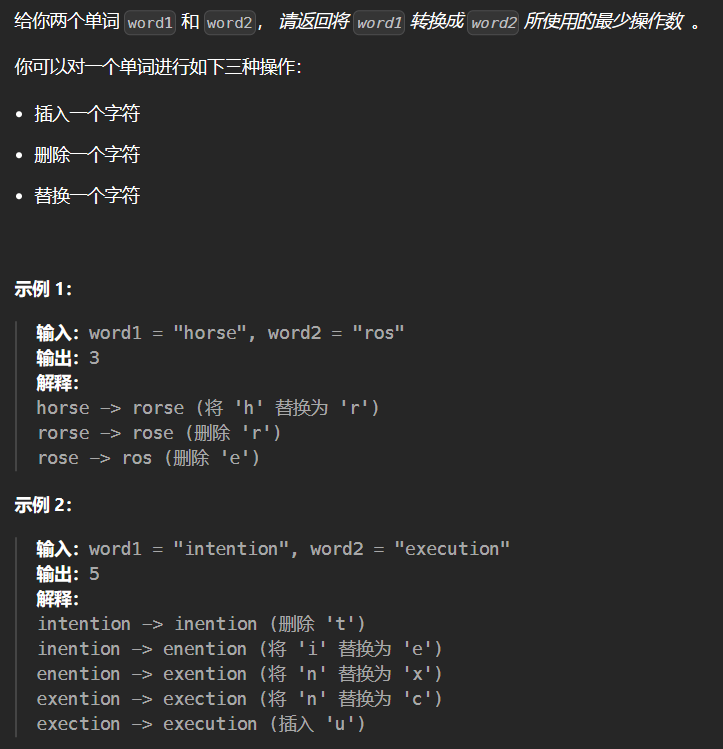
5.10 72-编辑距离

72

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int minDistance(string word1, string word2) {
        int size1 = word1.size();
        int size2 = word2.size();
        vector<vector<int>> dp(size1+1,vector<int>(size2+1));
        for(int i = 0; i <= size1; ++i)
            dp[i][0] = i;
        for(int i = 0; i <= size2; ++i)
            dp[0][i] = i;
        
        for(int i = 1; i <= size1; ++i)
        {
            for(int j = 1; j <= size2; ++j)
            {
                if(word1[i-1] == word2[j-1])
                    dp[i][j] = dp[i-1][j-1];
                else
                    dp[i][j] = min(dp[i-1][j],min(dp[i][j-1],dp[i-1][j-1])) + 1;
            }
        }
        return dp[size1][size2];
    }
};

5.11 647-回文子串

647

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    int countSubstrings(string s) {
        int size = s.size();
        vector<vector<bool>> dp(size,vector<bool>(size,false));
        int ans = 0;
        for(int i = size-1; i >= 0; i--)
        {
            for(int j = i; j < size; ++j)
            {
                if(s[i] == s[j])
                {
                    if(j-i <= 1) //aa || a
                    {
                        ans++;
                        dp[i][j] = true;
                    }
                    else if(dp[i+1][j-1]) // aba 再通过dp判断
                    {
                        ans++;
                        dp[i][j] = true;
                    }
                }
            }
        }
        return ans;
    }
};

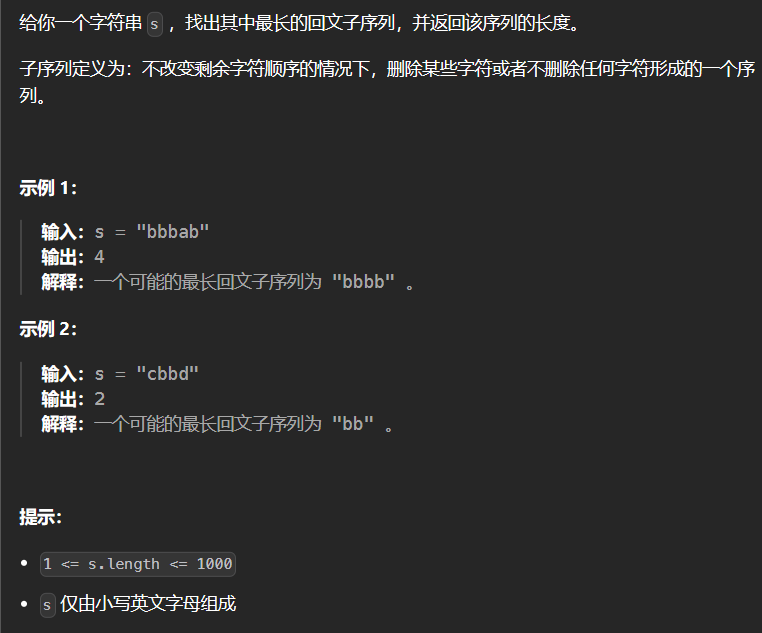
5.12 516-最长回文子序列

516

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int longestPalindromeSubseq(string s) {
        int size = s.size();
        vector<vector<int>> dp(size,vector<int>(size,0));
        for(int i = 0; i < size; ++i)
            dp[i][i] = 1;

        for(int i = size-1; i >= 0; --i)
        {
            for(int j = i+1; j < size; ++j)
            {
                if(s[i] == s[j])
                    dp[i][j] = dp[i+1][j-1]+2;
                else
                    dp[i][j] = max(dp[i+1][j],dp[i][j-1]);
            }
        }
        return dp[0][size-1];
    }
};