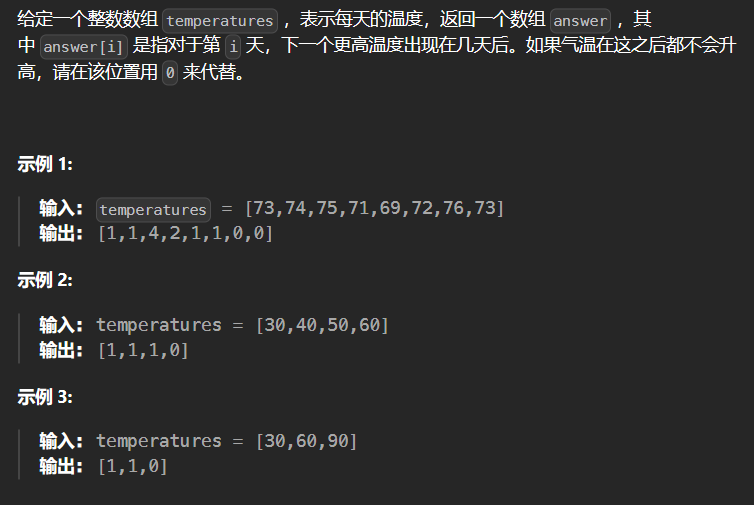
1. 单调栈# 1.1 739-每日温度

739

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    vector<int> dailyTemperatures(vector<int>& temperatures) {
        int size = temperatures.size();
        stack<int> st;
        st.push(0);
        vector<int> ans(size,0); //初始化为0,防止后续计算的递减导致无法找到而无法赋值
        for(int i = 1; i < size; ++i)
        {
            if(temperatures[i] < temperatures[st.top()])
                st.push(i);
            else if(temperatures[i] == temperatures[st.top()])
                st.push(i);
            else
            {
                while(!st.empty() && temperatures[i] > temperatures[st.top()])
                {
                    ans[st.top()] = i - st.top(); //计算距离后入数组
                    st.pop(); //弹出
                }
                st.push(i);
            }
        }
        return ans;
    }
};

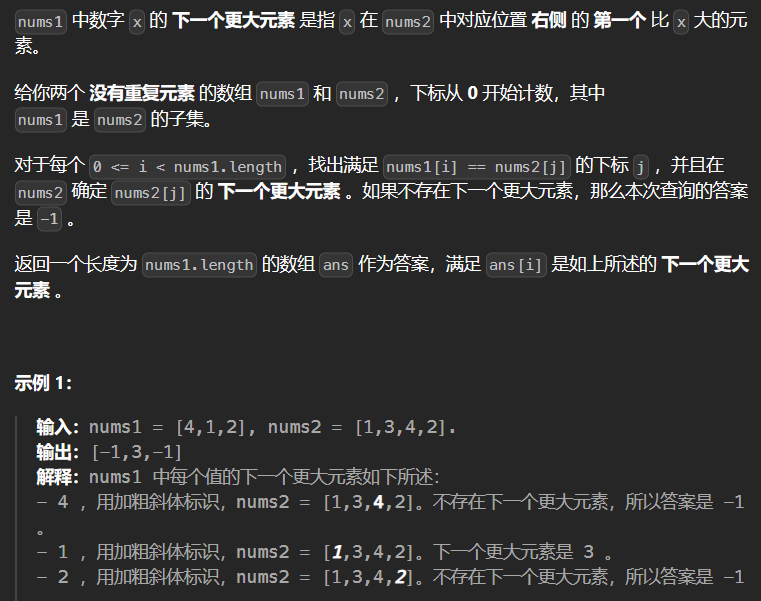
1.2 496-下一个更大元素 I

496

类似于上一题,且精简版的写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
        int size1 = nums1.size();
        int size2 = nums2.size();
        vector<int> ans(size1,-1);
        if(size1 == 0)
            return ans;
        stack<int> st;

        unordered_map<int,int> um; //key为下标元素, value为index
        for(int i = 0; i < size1; ++i)
            um[nums1[i]] = i;
        st.push(0);

        for(int i = 1; i < size2; ++i)
        {
            while(!st.empty() && nums2[i] > nums2[st.top()])
            {
                if(um.count(nums2[st.top()]) > 0) //哈希内有对应num2的元素
                {
                    int index = um[nums2[st.top()]]; //index为num1中较小元素的坐标
                    ans[index] = nums2[i];
                }
                st.pop();
            }
            st.push(i);
        }
        return ans;
    }
};

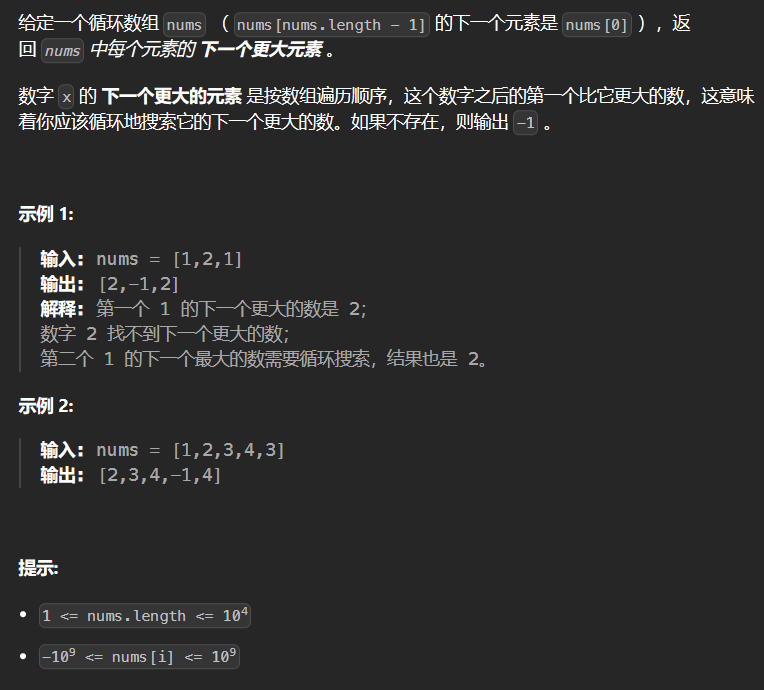
1.3 503-下一个最大元素 II

503

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    vector<int> nextGreaterElements(vector<int>& nums) {
        int size = nums.size();
        stack<int> st;
        vector<int> ans(size,-1);
        st.push(0);
        for(int i = 1; i < size*2; ++i)
        {
            if(nums[i % size] < nums[st.top()])
                st.push(i % size);
            else
            {
                while(!st.empty() && nums[i % size] > nums[st.top()])
                {
                    ans[st.top()] = nums[i % size];
                    st.pop();
                }
                st.push(i % size);
            }
        }
        return ans;
    }
};

1.4* 42-接雨水

42

…

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int trap(vector<int>& height) {
        int size = height.size();
        stack<int> st;
        st.push(0);
        int ans = 0;
        for(int i = 1; i < size; ++i)
        {
            while(!st.empty() && height[i] > height[st.top()])
            {
                int mid = st.top();
                st.pop();
                if(!st.empty())
                {
                    int h = min(height[st.top()], height[i]) - height[mid];
                    int w = i - st.top() - 1;
                    ans += h*w;
                }
            }
            st.push(i); //求右边第一个更大元素,所以单调栈是递增的
        }
        return ans;
    }
};

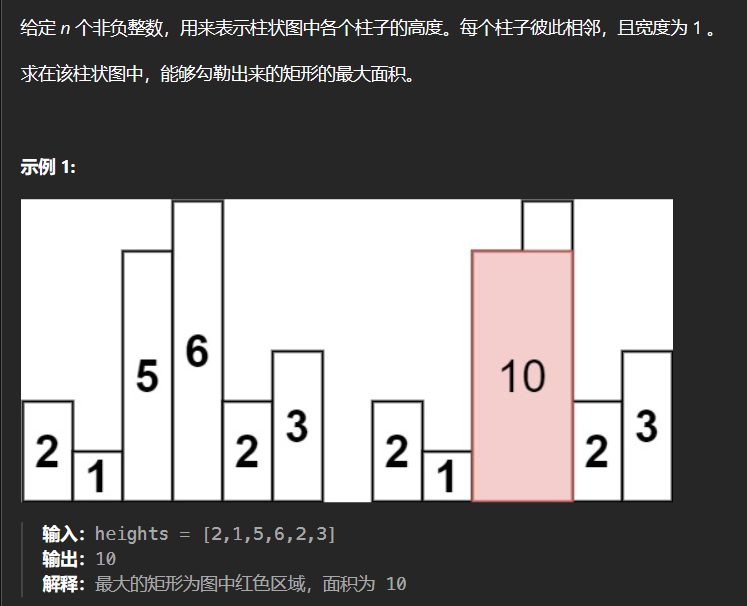
1.5* 84-柱状图中最大的矩形

84

…

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        stack<int> st;
        heights.insert(heights.begin(),0);
        heights.push_back(0);
        st.push(0);
        int ans = 0;
        int size = heights.size();
        for(int i = 1; i < size; ++i)
        {
            while(heights[i] < heights[st.top()])
            {
                int mid = st.top();
                st.pop();
                int w = i - st.top() - 1;
                int h = heights[mid];
                ans = max(ans, w*h);
            }
            st.push(i);
        }
        return ans;
    }
};

2. 索引相关

2.1 1365-有多少小于当前数字的数字

1365

1
2
3
4
5
6
7
8
9
10
11
12
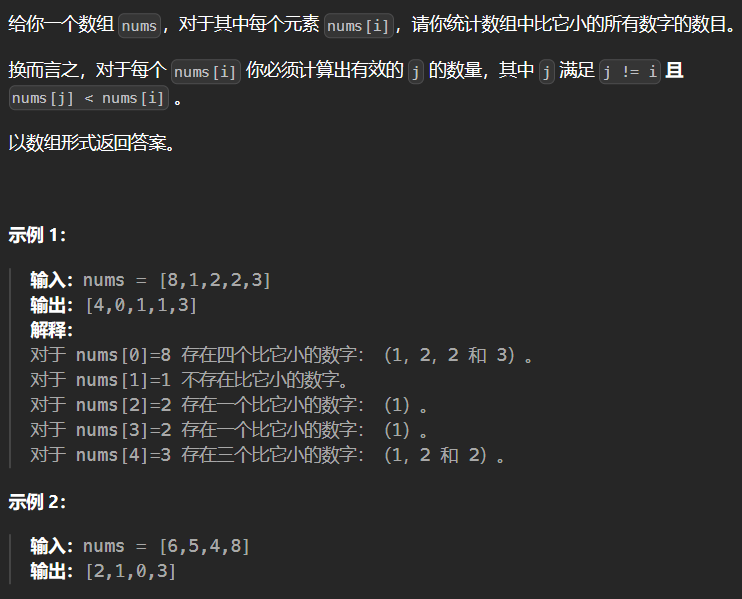
13
class Solution {
public:
    vector<int> smallerNumbersThanCurrent(vector<int>& nums) {
        vector<int> ans = nums;
        sort(ans.begin(), ans.end());
        int hash[101];
        for(int i = ans.size()-1; i>=0; --i)
            hash[ans[i]] = i; //元素值就是下标,下标就是大于本元素数值的个数
        for(int i = 0; i < nums.size(); ++i)
            ans[i] = hash[nums[i]];
        return ans;
    }
};

2.2 941-有效的山脉数组

941

满足以下条件为有效山脉zai

1
2
3
4
5
6
7
8
9
10
11
12
13
14
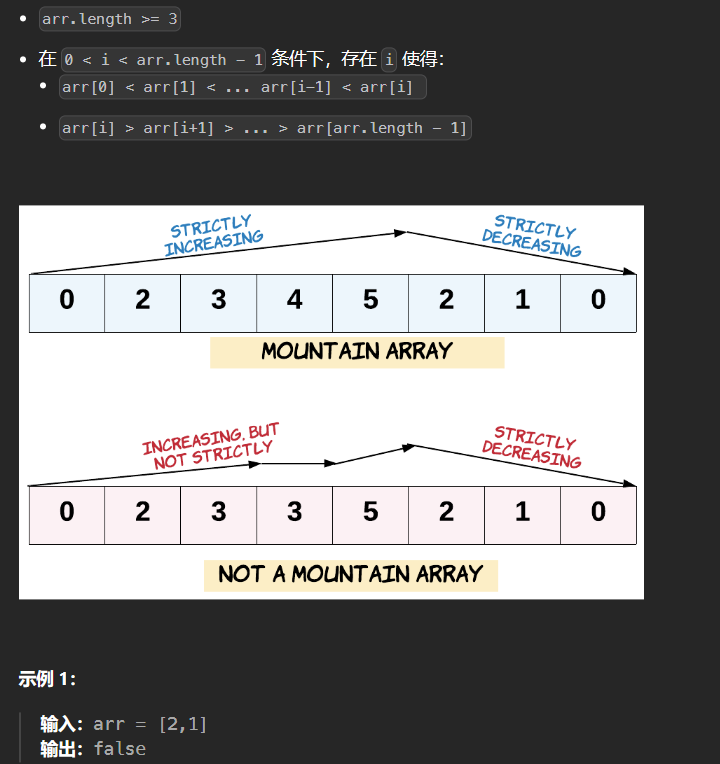
15
class Solution {
public:
    bool validMountainArray(vector<int>& arr) {
        int size = arr.size();
        int left = 0;
        int right = size - 1;
        while(left < size - 1 && arr[left] < arr[left+1])
            left++;
        while(right > 0 && arr[right] < arr[right-1])
            right--;
        if(left == right && left != 0 && right != size-1)
            return true;
        return false;
    }
};

2.3 1207-独一无二的出现次数

1207

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
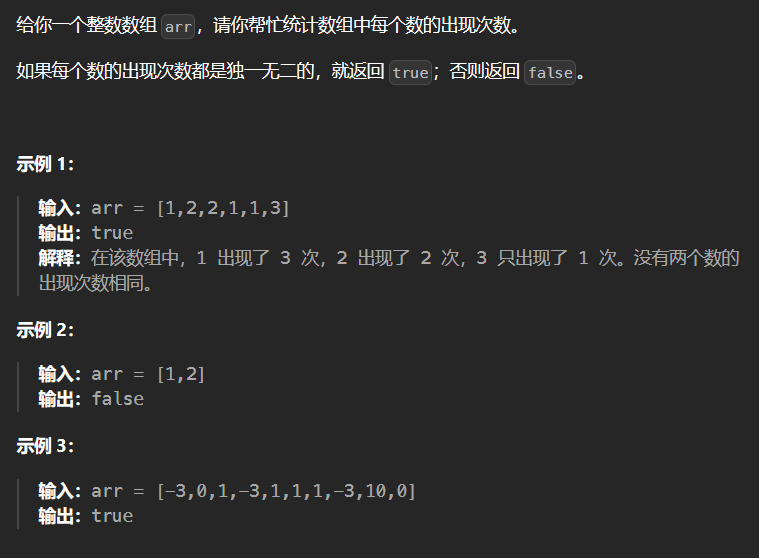
21
class Solution {
public:
    bool uniqueOccurrences(vector<int>& arr) {
        int hash[2002] = {0};
        for(auto e : arr)
            hash[e + 1000]++; //记录频率

        bool frequent[1002] = {false}; //记录相同频率是否出现
        for(int i = 0 ; i <= 2000; ++i)
        {
            if(hash[i]) //如果这个数字出现过
            {
                if(frequent[hash[i]] == false) //记录此频率
                    frequent[hash[i]] = true;
                else
                    return false; //频率被记录过直接返回
            }
        }
        return true;
    }
};

2.4 283-移动零

283

1
2
3
4
5
6
7
8
9
10
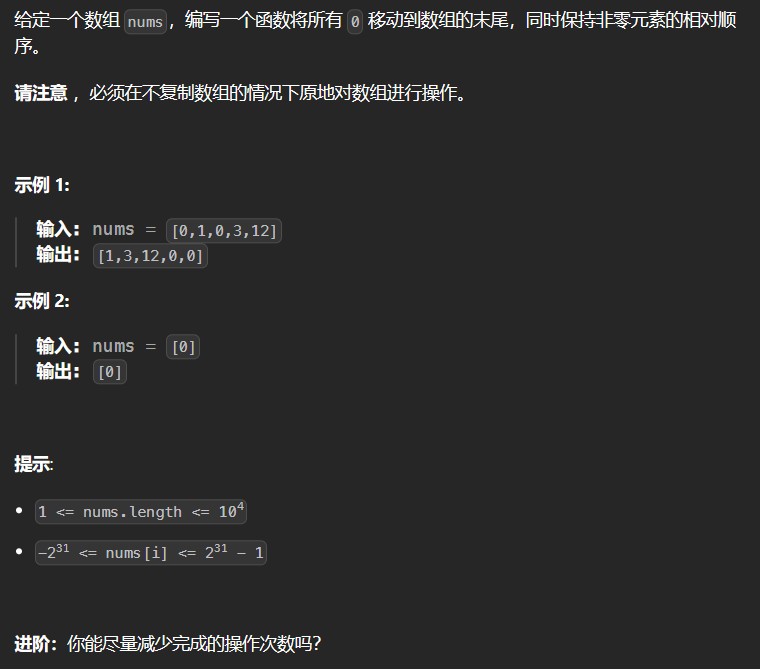
11
class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int slowindex = 0;
        for(int fastindex = 0; fastindex < nums.size(); fastindex++)
            if(nums[fastindex] != 0) //元素==0 快指针向前
                nums[slowindex++] = nums[fastindex];
        for(int i = slowindex; i < nums.size(); ++i)
            nums[i] = 0;
    }
};

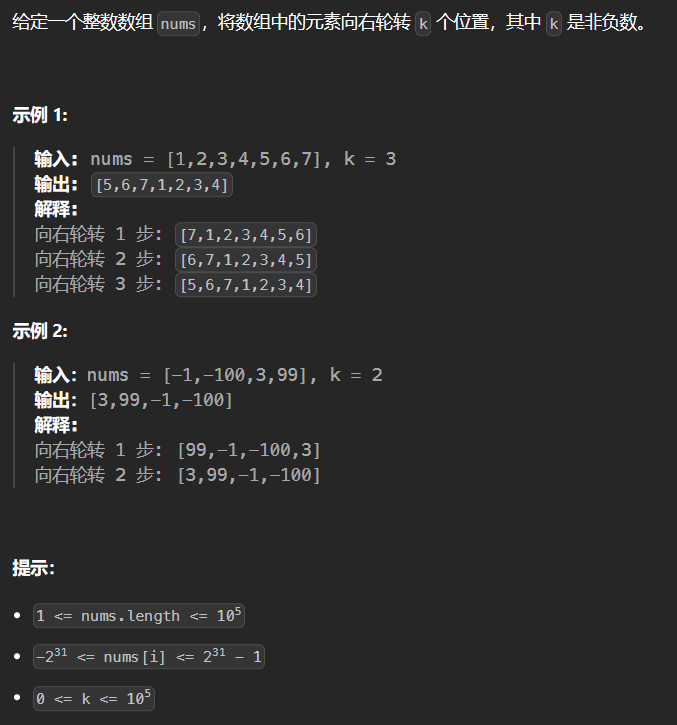
2.5 189-轮转数组

189

1
2
3
4
5
6
7
8
9
class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        k = k % nums.size();
        reverse(nums.begin(),nums.end());
        reverse(nums.begin(),nums.begin()+k);
        reverse(nums.begin()+k,nums.end());
    }
};

2.6 724-寻找数组的中心下标

724

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int pivotIndex(vector<int>& nums) {
        int sum = 0;
        for(int num : nums)
            sum += num; 
        int leftsum = 0; 
        int rightsum = 0; 
        for(int i = 0; i < nums.size(); ++i)
        {
            leftsum += nums[i]; //左边+中间
            rightsum = sum - leftsum + nums[i]; //右边+中间
            if(leftsum == rightsum)
                return i;
        }
        return -1;
    }
};

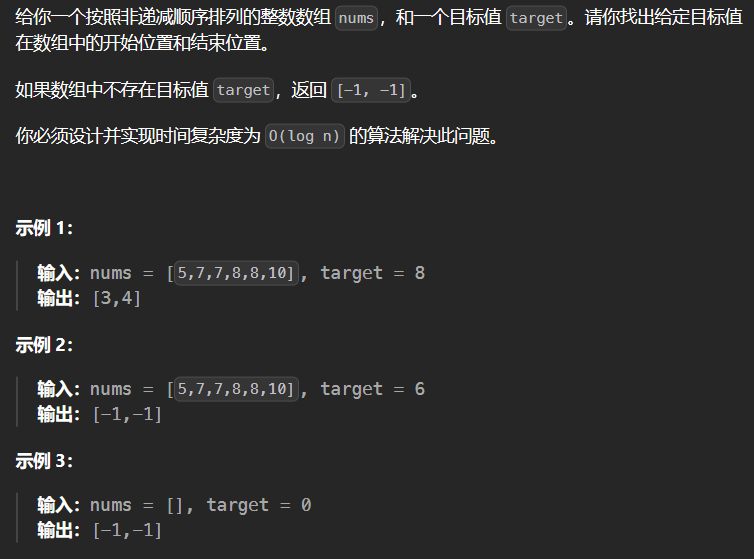
2.7 34-在排序数组中查找元素的第一个和最后一个位置

34

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        int leftBorder = getLeftBorder(nums, target);
        int rightBorder = getRightBorder(nums, target);
        // 情况1 : 没有找到(target跑到边界外,循环都没有进入)
        if (leftBorder == -2 || rightBorder == -2)  
            return {-1, -1};
        // 情况三
        if (rightBorder - leftBorder > 1) 
            return {leftBorder + 1, rightBorder - 1};
        // 情况2 : 进入循环内部但是找不到
        return {-1, -1};
    }
private:
     int getRightBorder(vector<int>& nums, int target) 
     {
        int left = 0;
        int right = nums.size() - 1;
        int rightBorder = -2; // 记录一下rightBorder没有被赋值的情况
        while (left <= right) 
        {
            int middle = left + ((right - left) / 2);
            if (nums[middle] > target) 
            {
                right = middle - 1;
            } 
            else 
            { // 寻找右边界，nums[middle] == target的时候更新left
                left = middle + 1;
                rightBorder = left;
            }
        }
        return rightBorder;
    }
    int getLeftBorder(vector<int>& nums, int target) 
    {
        int left = 0;
        int right = nums.size() - 1;
        int leftBorder = -2; // 记录一下leftBorder没有被赋值的情况
        while (left <= right) 
        {
            int middle = left + ((right - left) / 2);
            if (nums[middle] >= target) 
            { // 寻找左边界，nums[middle] == target的时候更新right
                right = middle - 1;
                leftBorder = right;
            } 
            else 
            {
                left = middle + 1;
            }
        }
        return leftBorder;
    }
};

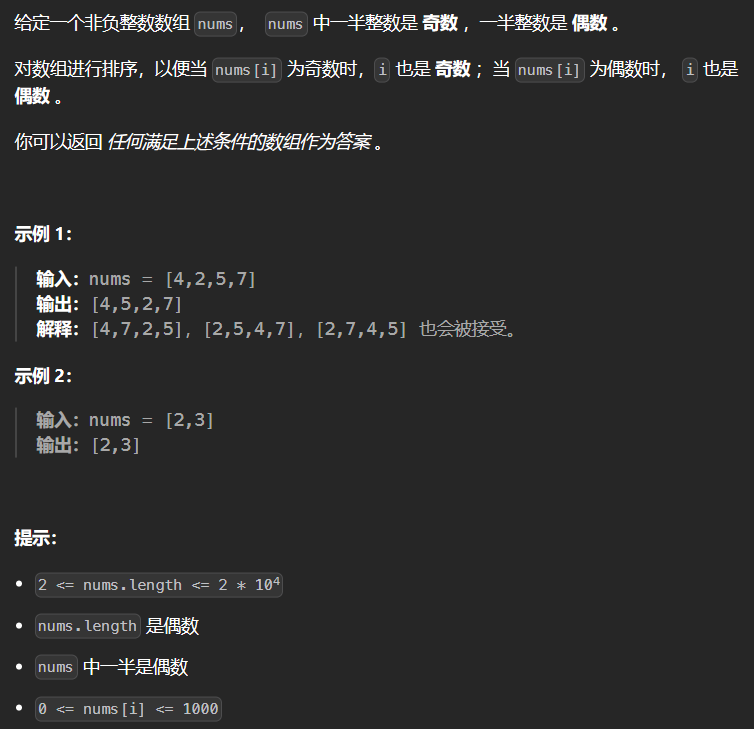
2.8 922-按奇偶排序数组

922

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    vector<int> sortArrayByParityII(vector<int>& nums) {
        int oddindex = 1; //奇数位
        for(int i = 0; i < nums.size(); i+=2)
        {
            if(nums[i] % 2 == 1) //偶数为遇到奇数
            {
                while(nums[oddindex] % 2 != 0) //如果奇数位也是偶数
                    oddindex += 2;
                swap(nums[i],nums[oddindex]); //替换
            }
        }
        return nums;
    }
};

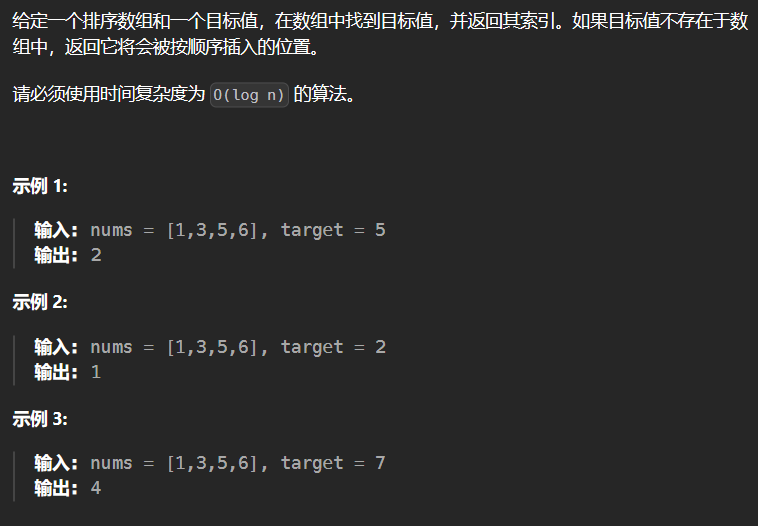
2.9 35-搜索插入位置

35

双闭区间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1;
        while(left <= right) //left == right 区间[left,right]仍然有效
        {
            int mid = left + (right - left) / 2;
            if(nums[mid] == target)
                return mid;
            else if(nums[mid] < target)
                left = mid + 1;
            else
                right = mid - 1;
        }
        return right+1;
    }
};

单开区间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int n = nums.size();
        int left = 0;
        int right = n; // 定义target在左闭右开的区间里，[left, right)  target
        while (left < right) // 因为left == right的时候，在[left, right)无效
        { 
            int middle = left + ((right - left) >> 1);
            if (nums[middle] > target)
                right = middle; // target 在左区间，在[left, middle)中
            else if (nums[middle] < target)
                left = middle + 1; // target 在右区间，在 [middle+1, right)中
            else  // nums[middle] == target
                return middle; // 数组中找到目标值的情况，直接返回下标
        }
        return right;
    }
};

3. 链表

3.1 24-两两交换链表中的节点

24

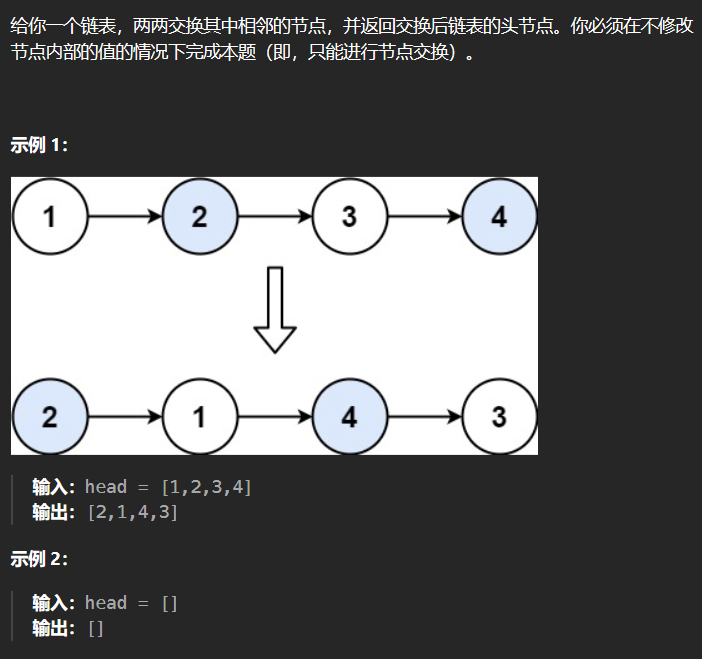
迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        if(!head || !head->next)
            return head;
        ListNode* solider = new ListNode(0); //头部创建一个新节点
        solider->next = head;

        ListNode* temp = solider;
        while(temp->next && temp->next->next)
        {
            ListNode* node1 = temp->next;
            ListNode* node2 = temp->next->next;
            temp->next = node2;
            node1->next = node2->next;
            node2->next = node1;
            temp = node1;
        }
        ListNode* ans = solider->next;
        delete solider;
        return ans;
    }
};

3.2 234-回文链表

234

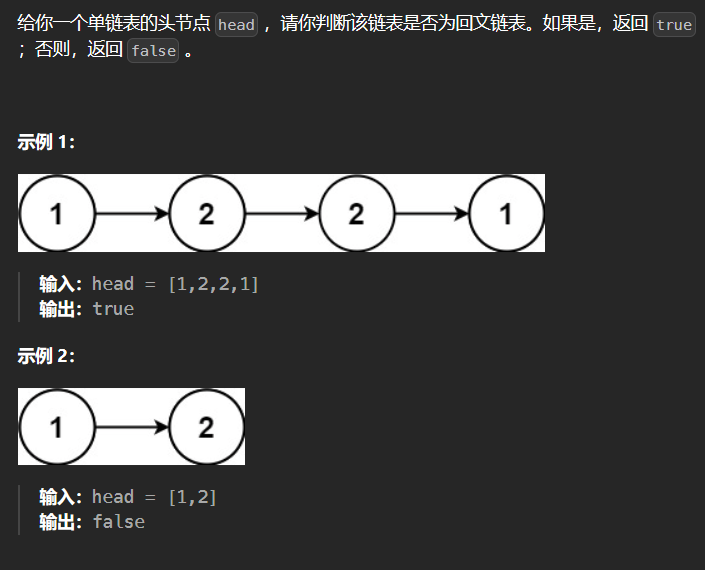
O(N) 时间复杂度, O(1) 空间复杂度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
public:
     ListNode* reverseList(ListNode* head) //反转链表
     {
        ListNode* prev = nullptr;
        ListNode* curr = head;
        while (curr) 
        {
            ListNode* next = curr->next;
            curr->next = prev;
            prev = curr;
            curr = next; //向前递进
        }
        return prev;
    }

    ListNode* endOfFirstHalf(ListNode* head) 
    {
        ListNode* fast = head;
        ListNode* slow = head;
        while (fast->next && fast->next->next) 
        {
            fast = fast->next->next;
            slow = slow->next;
        }
        return slow;
    }
    bool isPalindrome(ListNode* head) {
        if(!head)
            return true;
        //找到前半部分链表的尾节点并反转后半部分
        ListNode* first_half_end = endOfFirstHalf(head); //前半部分的尾节点
        ListNode* second_half_start = reverseList(first_half_end->next); //反转后的头节点

        ListNode* p1 = head; //最左
        ListNode* p2 = second_half_start; //最右
        bool ans = true;
        while(ans && p2)
        {
            if(p1->val != p2->val)
                return false;
            p1 = p1->next;
            p2 = p2->next;
        }
        first_half_end->next = reverseList(second_half_start); //重新接好
        return ans;
    }
};

3.3 143-重排链表

134

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
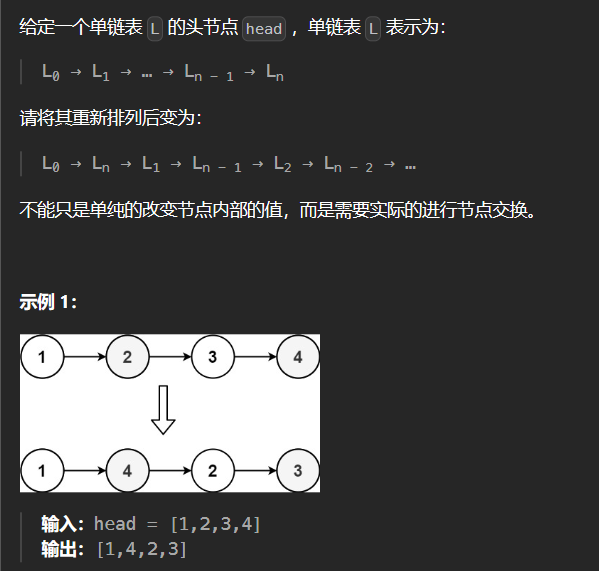
53
class Solution {
public:
    ListNode* middleNode(ListNode* head) //返回中间节点(左)
    {
        ListNode* slow = head;
        ListNode* fast = head;
        while (fast->next  && fast->next->next ) 
        {
            slow = slow->next;
            fast = fast->next->next;
        }
        return slow;
    }

    ListNode* reverseList(ListNode* head) //反转链表
    {
        ListNode* prev = nullptr;
        ListNode* curr = head;
        while (curr) 
        {
            ListNode* nextTemp = curr->next;
            curr->next = prev;
            prev = curr;
            curr = nextTemp;
        }
        return prev;
    }

    void mergeList(ListNode* l1, ListNode* l2) //交叉合并链表
    {
        ListNode* l1_tmp;
        ListNode* l2_tmp;
        while (l1  && l2 ) 
        {
            l1_tmp = l1->next;
            l2_tmp = l2->next;

            l1->next = l2;
            l1 = l1_tmp;

            l2->next = l1;
            l2 = l2_tmp;
        }
    }
    void reorderList(ListNode* head) {
        ListNode* mid = middleNode(head);
        ListNode* l1 = head;
        ListNode* l2 = mid->next; //后半部分的头节点
        mid->next = nullptr;      //断开两半连接
        l2 = reverseList(l2);     //反转后半部分
        mergeList(l1, l2);        //交叉连接两部分
    }
};

3.4 141-环形列表

141

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
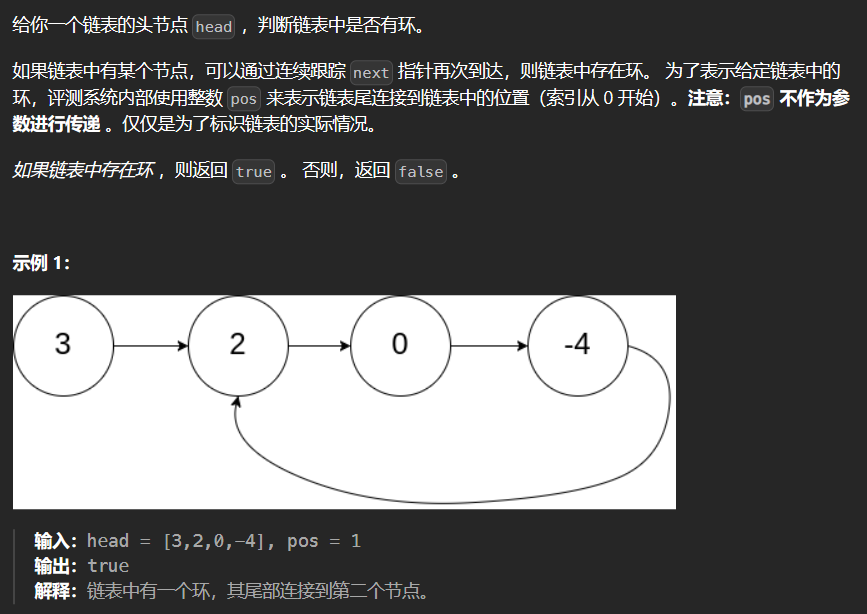
17
class Solution {
public:
    bool hasCycle(ListNode *head) {
        if(!head)
            return false;
        ListNode* slow = head;
        ListNode* fast = head;
        while(fast->next && fast->next->next)
        {
            slow = slow->next;
            fast = fast->next->next;
            if(slow == fast)
                return true;
        }
        return false;
    }
};

3.5 面试题02.07-链表相交

02.07

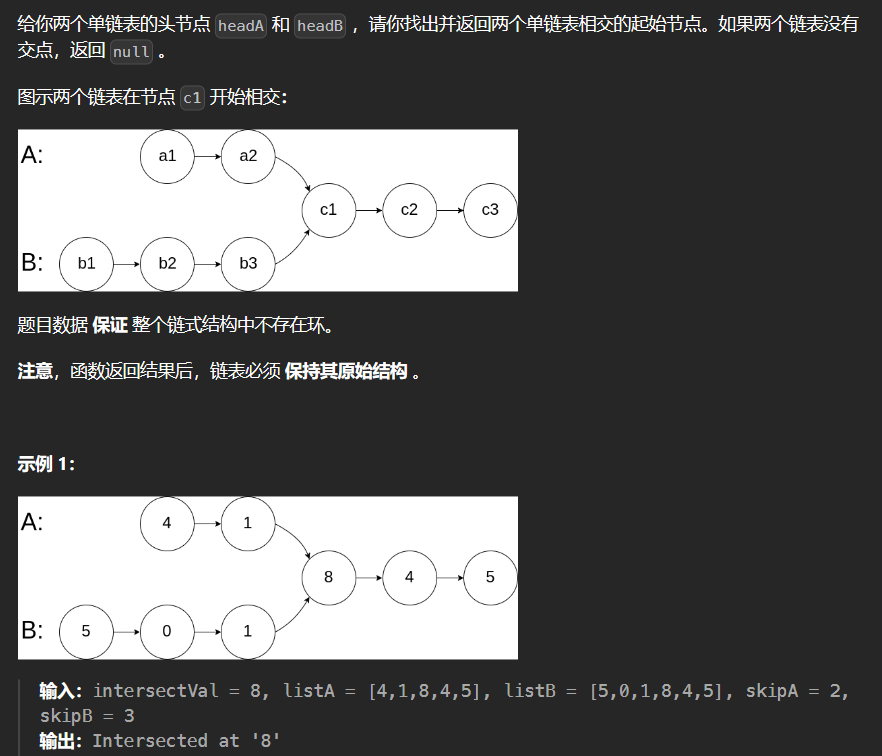
时间复杂度为O(N),空间复杂度为O(1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        if(!headA || !headB)
            return nullptr;
        ListNode* pa = headA;
        ListNode* pb = headB;
        while(pa != pb) 
        {
            pa = !pa ? headB : pa->next;
            pb = !pb ? headA : pb->next;
        }
        //核心思想是,链表走过头后再重置为另一条链表,依次之间的差距会在第二次遍历后为0
        return pa;
    }
};

4. 哈希表

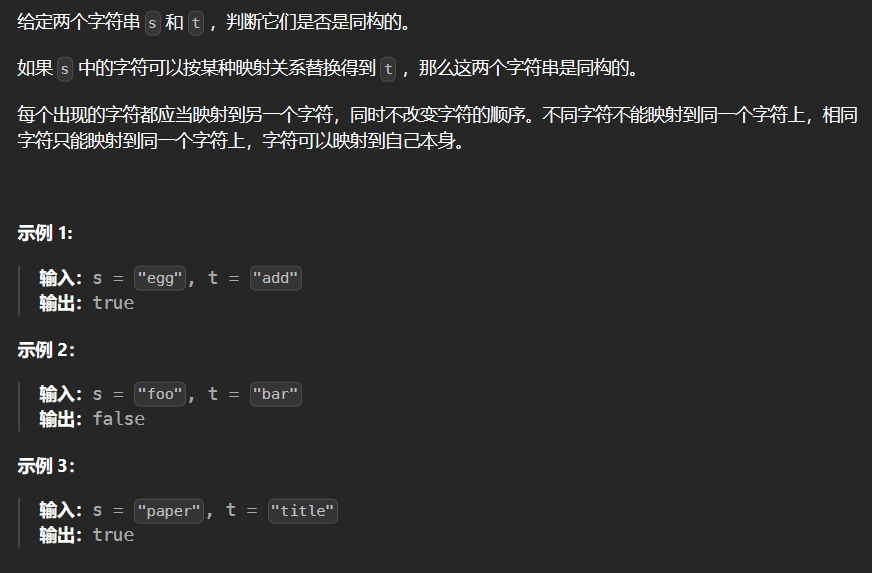
4.1 205-同构字符串

205

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    bool isIsomorphic(string s, string t) {
        unordered_map<char,char> um1;
        unordered_map<char,char> um2;
        int size = s.size();
        for(int i = 0; i < size; ++i)
        {
            char x = s[i];
            char y = t[i];
            //遇见过(重复使用了),并且对方字符串没有使用相对应的字符
            if((um1.count(x) && um1[x] != y) || 
                (um2.count(y) && um2[y] != x))
                return false;
            um1[x] = y;
            um2[y] = x;
        }    
        return true;
    }
};

5. 字符串

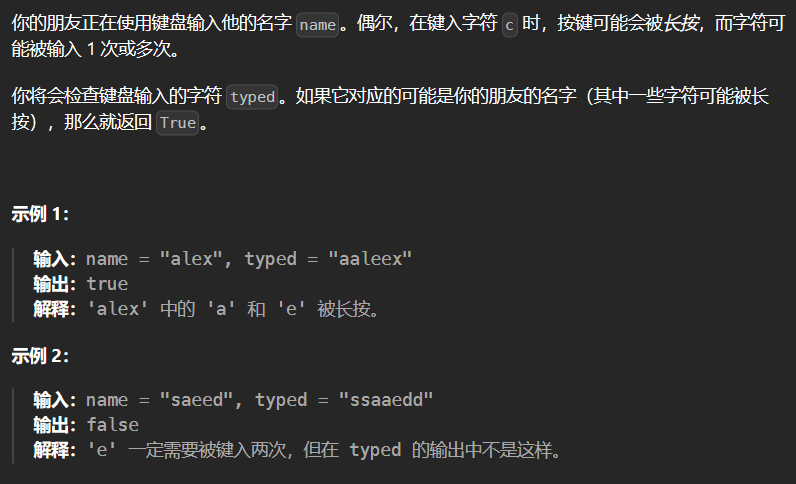
5.1 925-长按键入

925

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    bool isLongPressedName(string name, string typed) {
        int i = 0;
        int j = 0;
        while(j < typed.size())
        {
            if(i < name.size() && name[i] == typed[j])
            {
                i++;
                j++;
            }
            else if(j > 0 && typed[j] == typed[j - 1]) //如果要长按
                j++;
            else
                return false;
        }
        return i == name.size(); //name走完了就true
    }
};

5.2 844-比较含退格的字符串

844

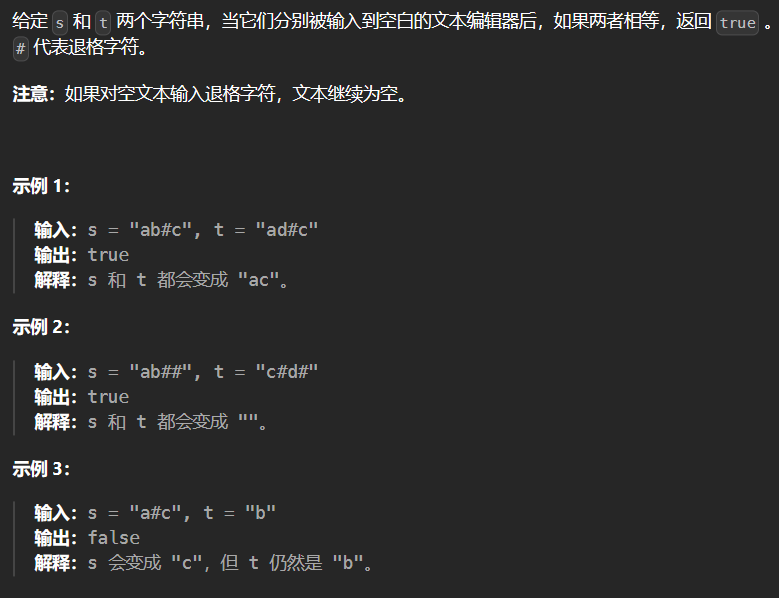
时间复杂度为O(N), 空间复杂度为O(1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
class Solution {
public:
    bool backspaceCompare(string s, string t) {
        int i = s.size() - 1;
        int j = t.size() - 1;
        int skips = 0;
        int skipt = 0;
        while(i >= 0 || j >= 0)
        {
            while(i >= 0)
            {
                if(s[i] == '#')
                {
                    skips++;
                    i--;
                }
                else if(skips > 0)
                {
                    skips--;
                    i--;
                }
                else
                    break;
            }
            while(j >= 0)
            {
                if(t[j] == '#')
                {
                    skipt++;
                    j--;
                }
                else if(skipt > 0)
                {
                    skipt--;
                    j--;
                }
                else
                    break;
            }
            if(i >= 0 && j >= 0)
            {
                if(s[i] != t[j])
                    return false;
            }
            else
                if(i>=0 || j>=0)
                    return false;
            i--;
            j--;
        }
        return true;
    }

};

6. 二叉树

6.1 129-求根节点到叶节点数字之和

129

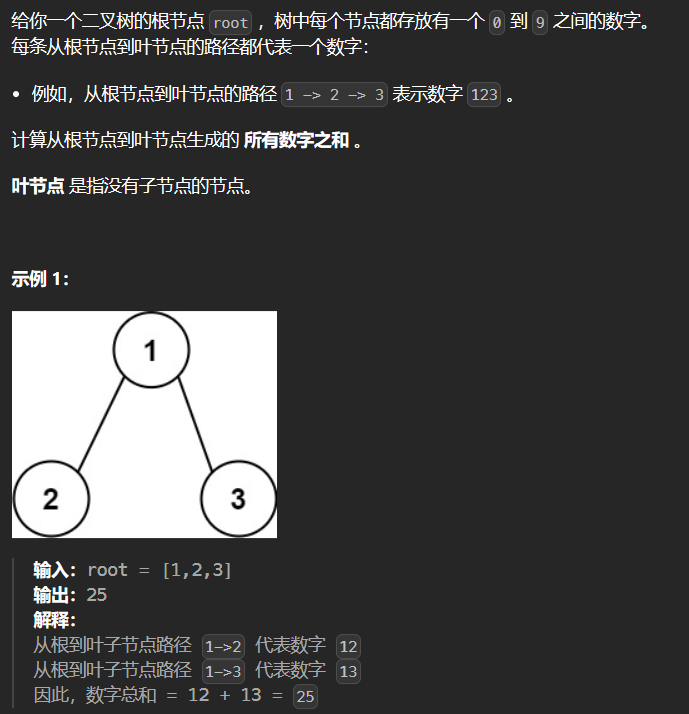
dfs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int Recursion(TreeNode* root, int prevsum)
    {
        if(!root)
            return 0;
        int sum = prevsum*10 + root->val;
        
        if(!root->left && !root->right)
            return sum;
        else
            return Recursion(root->left,sum) + Recursion(root->right,sum);
    }
    int sumNumbers(TreeNode* root) {
        return Recursion(root,0);
    }
};

6.2 1382-将二叉搜索树变平衡

1382

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
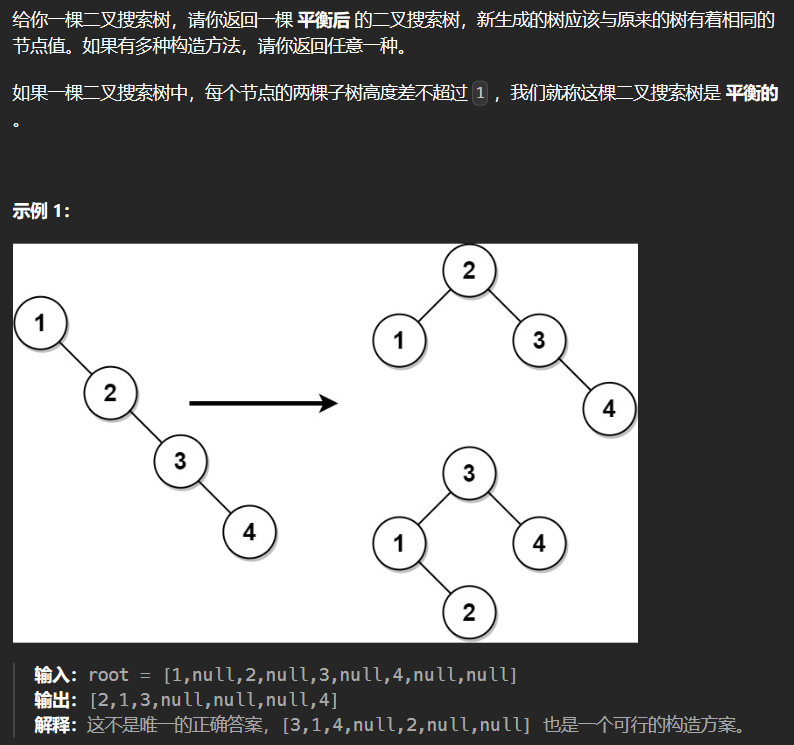
28
class Solution {
public:
    vector<int> vec;
    void Traversal(TreeNode* cur) //将有序树转换为有序数组
    {
        if(!cur)
            return;
        Traversal(cur->left);
        vec.push_back(cur->val);
        Traversal(cur->right);
    }

    //将有序数组转换为平衡二叉树
    TreeNode* GetTree(vector<int>& nums, int left, int right)
    {
        if(left > right)
            return nullptr;
        int mid = left + (right-left) / 2;
        TreeNode* root = new TreeNode(nums[mid]);
        root->left = GetTree(nums, left, mid-1);
        root->right = GetTree(nums, mid+1, right);
        return root;
    }
    TreeNode* balanceBST(TreeNode* root) {
        Traversal(root);
        return GetTree(vec, 0, vec.size() - 1);
    }
};

6.3 100-相同的树

100

1
2
3
4
5
6
7
8
9
10
11
12
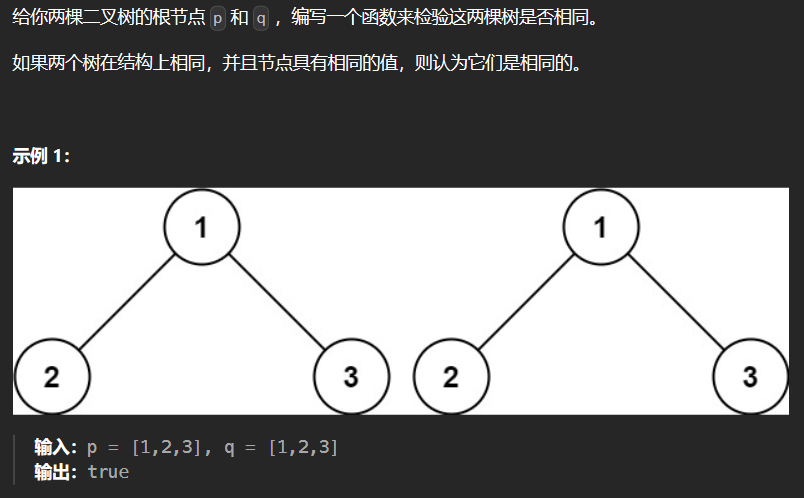
13
class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if(!p && !q)
            return true;
        else if(!p || !q) //一个有一个没有
            return false;
        else if(p->val != q->val)
            return false;
        else
            return isSameTree(p->left, q->left) && isSameTree(p->right,q->right);
    }
};

6.4 116-填充每个节点的下一个右侧节点指针

116

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
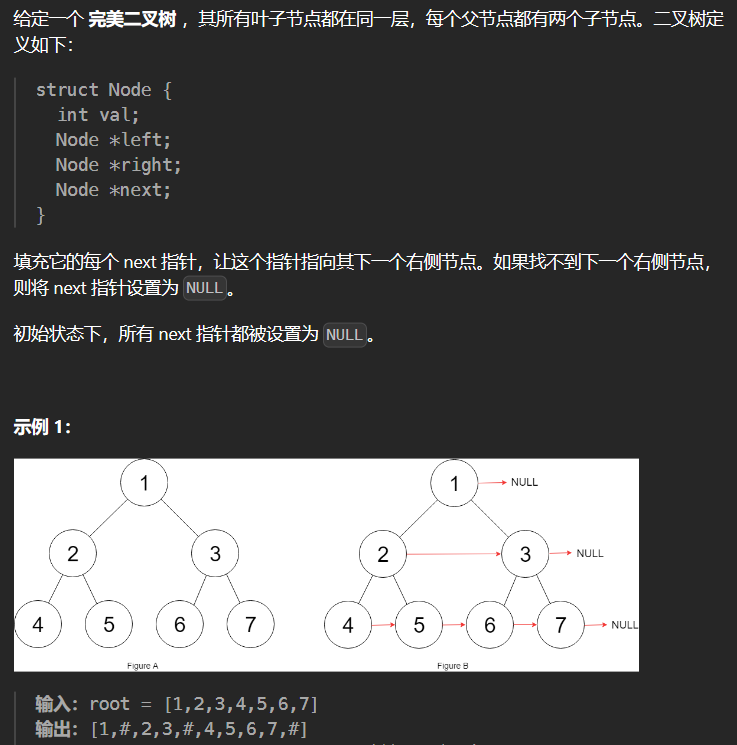
21
class Solution {
public:
    Node* connect(Node* root) {
        if(!root)
            return root;
        Node* leftmost = root;
        while(leftmost->left)
        {
            Node* head = leftmost;
            while(head)
            {
                head->left->next = head->right;
                if(head->next) //如果右边有节点
                    head->right->next = head->next->left;
                head = head->next;
            }
            leftmost = leftmost->left;
        }
        return root;
    }
};

7. 回溯算法

7.1* 52-N皇后II

52

…

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
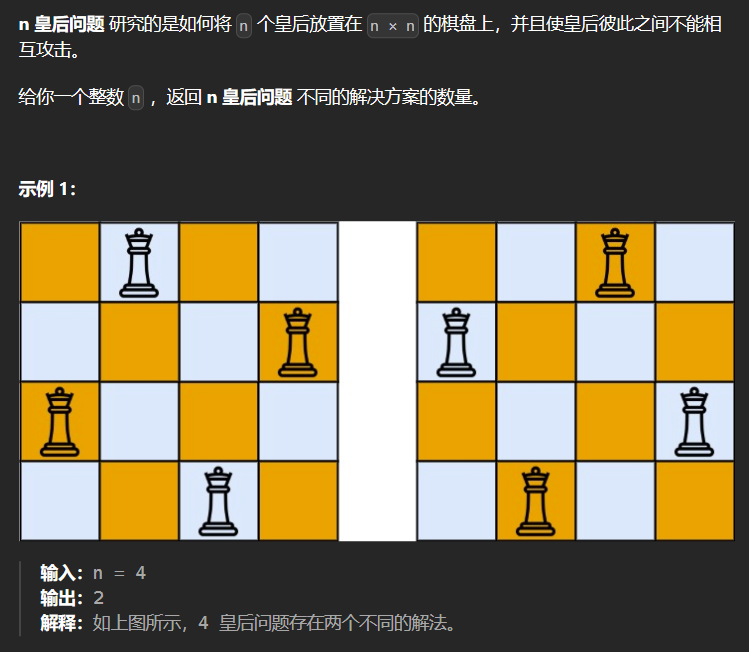
class Solution {
public:
    int totalNQueens(int n) {
        unordered_set<int> columns, diagonals1, diagonals2;
        return backtrack(n, 0, columns, diagonals1, diagonals2);
    }

    int backtrack(int n, int row, unordered_set<int>& columns, unordered_set<int>& diagonals1, unordered_set<int>& diagonals2) {
        if (row == n) 
            return 1;
        else 
        {
            int count = 0;
            for (int i = 0; i < n; i++) 
            {
                if (columns.find(i) != columns.end()) 
                    continue;
                
                int diagonal1 = row - i;
                if (diagonals1.find(diagonal1) != diagonals1.end()) 
                    continue;
                
                int diagonal2 = row + i;
                if (diagonals2.find(diagonal2) != diagonals2.end()) 
                    continue;
                
                columns.insert(i);
                diagonals1.insert(diagonal1);
                diagonals2.insert(diagonal2);
                count += backtrack(n, row + 1, columns, diagonals1, diagonals2);
                columns.erase(i);
                diagonals1.erase(diagonal1);
                diagonals2.erase(diagonal2);
            }
            return count;
        }
    }
};

8. 贪心算法

8.1 649-Dota2参议院

649

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
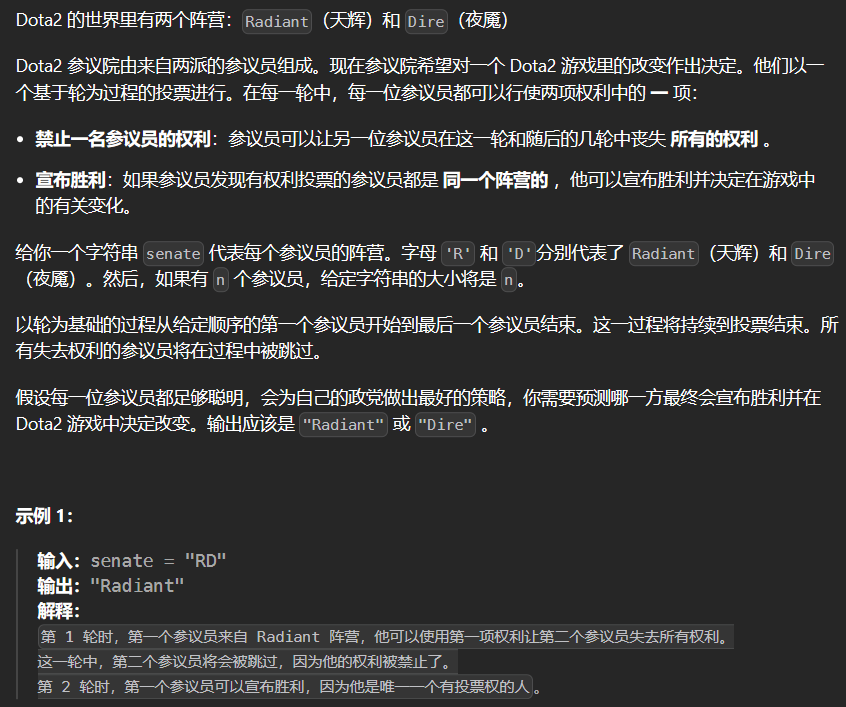
class Solution {
public:
    string predictPartyVictory(string senate) {
        // R = true表示本轮循环结束后，字符串里依然有R。D同理
        bool R = true;
        bool D = true;
        // 当flag大于0时，R在D前出现，R可以消灭D。
        // 当flag小于0时，D在R前出现，D可以消灭R
        int flag = 0;
        while (R && D) // 一旦R或者D为false，就结束循环，说明本轮结束后只剩下R或者D了
        { 
            R = false;
            D = false;
            for (int i = 0; i < senate.size(); i++) 
            {
                if (senate[i] == 'R') 
                {
                    if (flag < 0) 
                        senate[i] = 0; // 消灭R，R此时为false
                    else 
                        R = true; // 如果没被消灭，本轮循环结束有R
                    flag++;
                }
                if (senate[i] == 'D') 
                {
                    if (flag > 0) //前面有D
                        senate[i] = 0;
                    else 
                        D = true;
                    flag--;
                }
            }
        }
        // 循环结束之后，R和D只能有一个为true
        return R == true ? "Radiant" : "Dire";
    }
};

8.2 1221-分割平衡字符串

1221

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int balancedStringSplit(string s) {
        int ans = 0;
        int d = 0;
        for(char ch : s)
        {
            ch == 'L' ? ++d : --d;
            if(d == 0)
                ++ans;
        }
        return ans;
    }
};

9. 动态规划

9.1 5-最长回文子串

5

//

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class Solution {
public:
    string longestPalindrome(string s) 
    {
        int n = s.size();
        if (n < 2) 
            return s;

        int maxLen = 1;
        int begin = 0;
        // dp[i][j] 表示 s[i..j] 是否是回文串
        vector<vector<int>> dp(n, vector<int>(n));
        // 初始化：所有长度为 1 的子串都是回文串
        for (int i = 0; i < n; i++) 
            dp[i][i] = true;
        // 递推开始
        // 先枚举子串长度
        for (int L = 2; L <= n; L++) 
        {
            // 枚举左边界，左边界的上限设置可以宽松一些
            for (int i = 0; i < n; i++) 
            {
                // 由 L 和 i 可以确定右边界，即 j - i + 1 = L 得
                int j = L + i - 1;
                // 如果右边界越界，就可以退出当前循环
                if (j >= n) 
                    break;

                if (s[i] != s[j]) 
                    dp[i][j] = false;
                else 
                {
                    if (j - i < 3) 
                        dp[i][j] = true;
                    else 
                        dp[i][j] = dp[i + 1][j - 1];
                }

                // 只要 dp[i][L] == true 成立就表示子串 s[i..L] 是回文,此时记录回文长度和起始位置
                if (dp[i][j] && j - i + 1 > maxLen) 
                {
                    maxLen = j - i + 1;
                    begin = i;
                }
            }
        }
        return s.substr(begin, maxLen);
    }
};

9.2* 132-分割回文串II

132

//

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int minCut(string s) {
        int n = s.size();
        vector<vector<int>> g(n, vector<int>(n, true));

        for (int i = n - 1; i >= 0; --i) 
            for (int j = i + 1; j < n; ++j) 
                g[i][j] = (s[i] == s[j]) && g[i + 1][j - 1];

        vector<int> f(n, INT_MAX);
        for (int i = 0; i < n; ++i) 
        {
            if (g[0][i]) 
                f[i] = 0;
            else 
            {
                for (int j = 0; j < i; ++j)
                    if (g[j + 1][i]) 
                        f[i] = min(f[i], f[j] + 1);
            }
        }
        return f[n - 1];
    }
};

9.3 673-最长递增子序列的个数

673

//

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
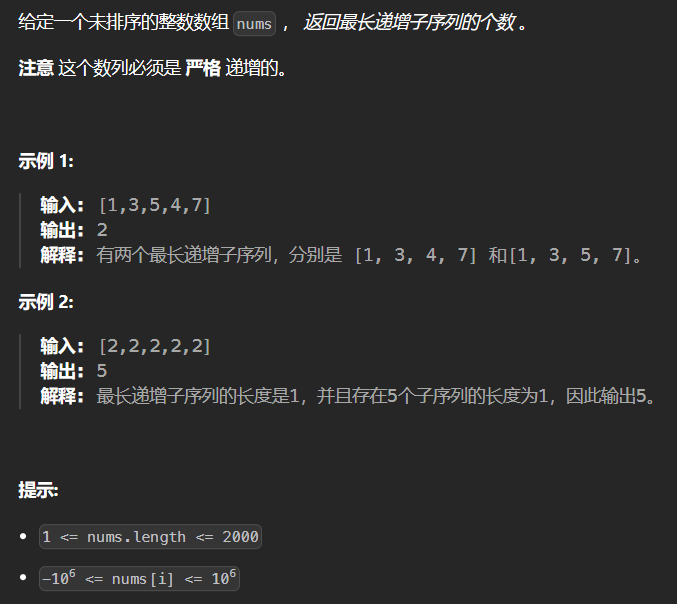
class Solution {
public:
    int findNumberOfLIS(vector<int> &nums) {
        int n = nums.size(), maxLen = 0, ans = 0;
        vector<int> dp(n), cnt(n);
        for (int i = 0; i < n; ++i) 
        {
            dp[i] = 1;
            cnt[i] = 1;
            for (int j = 0; j < i; ++j) 
            {
                if (nums[i] > nums[j]) 
                {
                    if (dp[j] + 1 > dp[i]) 
                    {
                        dp[i] = dp[j] + 1;
                        cnt[i] = cnt[j]; // 重置计数
                    } 
                    else if (dp[j] + 1 == dp[i]) 
                        cnt[i] += cnt[j];
                }
            }
            if (dp[i] > maxLen) 
            {
                maxLen = dp[i];
                ans = cnt[i]; // 重置计数
            } 
            else if (dp[i] == maxLen) 
                ans += cnt[i];
        }
        return ans;
    }
};

10. 图论

10.1 463-岛屿的周长

463

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class Solution {
public:
    int islandPerimeter(vector<vector<int>>& grid) {
        int sum = 0;    // 陆地数量
        int cover = 0;  // 相邻数量
        for (int i = 0; i < grid.size(); i++) 
        {
            for (int j = 0; j < grid[0].size(); j++) 
            {
                if (grid[i][j] == 1) 
                {
                    sum++;
                    // 统计上边相邻陆地
                    if(i - 1 >= 0 && grid[i - 1][j] == 1) 
                        cover++;
                    // 统计左边相邻陆地
                    if(j - 1 >= 0 && grid[i][j - 1] == 1)
                        cover++;
                    // 为什么没统计下边和右边？ 因为避免重复计算
                }
            }
        }
        return sum * 4 - cover * 2;
    }
};

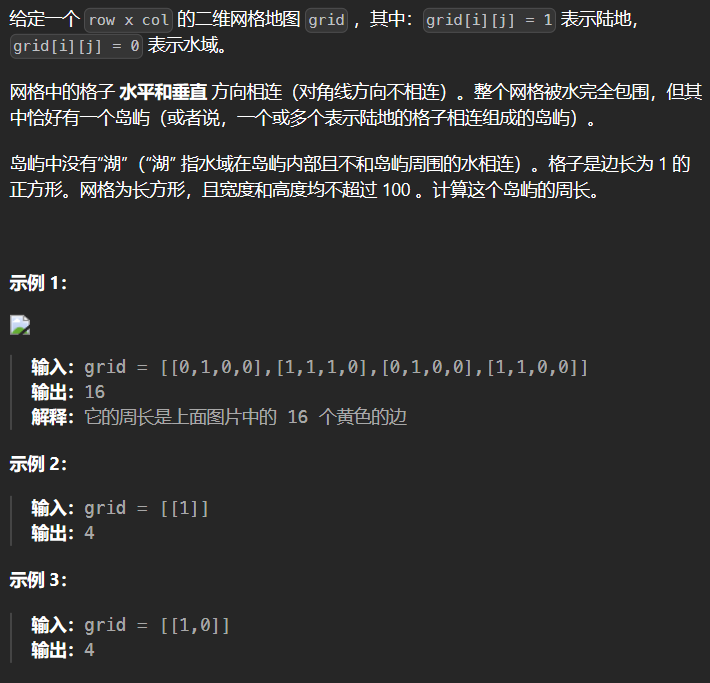
10.2 841-钥匙和房间

841

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
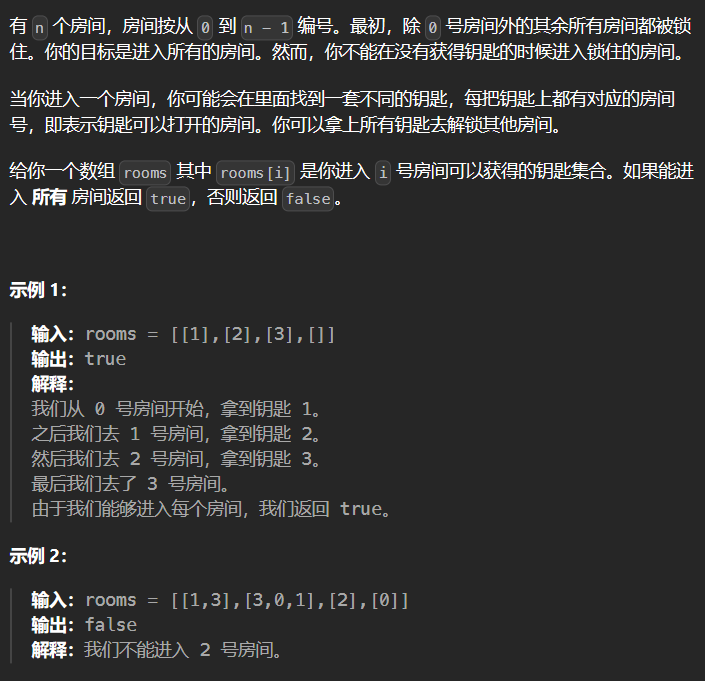
21
class Solution {
public:
    vector<int> vis;
    int num;

    void dfs(vector<vector<int>>& rooms, int x)
    {
        vis[x] = true;
        num++;
        for(auto& e : rooms[x])
            if(!vis[e]) //如果这个房间第一次有方法进入
                dfs(rooms,e);
    }
    bool canVisitAllRooms(vector<vector<int>>& rooms) {
        int size = rooms.size();
        num = 0;
        vis.resize(size); //必须初始化大小
        dfs(rooms,0);
        return num == size;
    }
};

10.3* 127-单词接龙

127

…

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
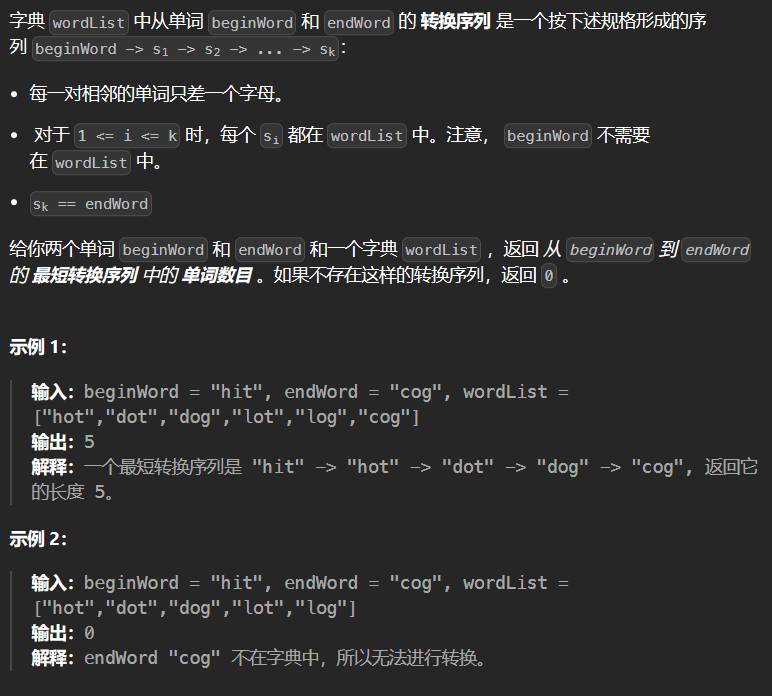
43
class Solution {
public:
    int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
        // 将vector转成unordered_set，提高查询速度
        unordered_set<string> wordSet(wordList.begin(), wordList.end());
        // 如果endWord没有在wordSet出现，直接返回0
        if (wordSet.find(endWord) == wordSet.end()) 
            return 0;
        // 记录word是否访问过
        unordered_map<string, int> visitMap; // <word, 查询到这个word路径长度>
        // 初始化队列
        queue<string> que;
        que.push(beginWord);
        // 初始化visitMap
        visitMap.insert(pair<string, int>(beginWord, 1));

        while(!que.empty()) 
        {
            string word = que.front();
            que.pop();
            int path = visitMap[word]; // 这个word的路径长度
            for (int i = 0; i < word.size(); i++) 
            {
                string newWord = word; // 用一个新单词替换word，因为每次置换一个字母
                for (int j = 0 ; j < 26; j++) 
                {
                    newWord[i] = j + 'a';
                    if (newWord == endWord) 
                        return path + 1; // 找到了end，返回path+1
                    // wordSet出现了newWord，并且newWord没有被访问过
                    if (wordSet.find(newWord) != wordSet.end()
                            && visitMap.find(newWord) == visitMap.end()) 
                    {
                        // 添加访问信息
                        visitMap.insert(pair<string, int>(newWord, path + 1));
                        que.push(newWord);
                    }
                }
            }
        }
        return 0;
    }
};

11. 并查集

11.1 684-冗余连接

684

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Solution {
private:
    int n = 1005; // 节点数量3 到 1000
    int father[1005];

    // 并查集初始化
    void init() 
    {
        for (int i = 0; i < n; ++i) 
            father[i] = i;
    }
    // 并查集里寻根的过程
    int find(int u) 
    {
        return u == father[u] ? u : father[u] = find(father[u]);
    }
    // 将v->u 这条边加入并查集
    void join(int u, int v) 
    {
        u = find(u);
        v = find(v);
        if (u == v) 
            return ;
        father[v] = u;
    }
    // 判断 u 和 v是否找到同一个根，本题用不上
    bool same(int u, int v) 
    {
        u = find(u);
        v = find(v);
        return u == v;
    }
public:
    vector<int> findRedundantConnection(vector<vector<int>>& edges) 
    {
        init();
        for (int i = 0; i < edges.size(); i++) 
        {
            if (same(edges[i][0], edges[i][1])) 
                return edges[i];
            else 
                join(edges[i][0], edges[i][1]);
        }
        return {};
    }
};

11.2* 685-冗余连接 II

685

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87

class Solution {
private:
    static const int N = 1010; // 如题：二维数组大小的在3到1000范围内
    int father[N];
    int n; // 边的数量
    // 并查集初始化
    void init() 
    {
        for (int i = 1; i <= n; ++i)
            father[i] = i;
    }
    // 并查集里寻根的过程
    int find(int u) 
    {
        return u == father[u] ? u : father[u] = find(father[u]);
    }
    // 将v->u 这条边加入并查集
    void join(int u, int v) 
    {
        u = find(u);
        v = find(v);
        if (u == v) 
            return ;
        father[v] = u;
    }
    // 判断 u 和 v是否找到同一个根
    bool same(int u, int v) 
    {
        u = find(u);
        v = find(v);
        return u == v;
    }
    // 在有向图里找到删除的那条边，使其变成树
    vector<int> getRemoveEdge(const vector<vector<int>>& edges) 
    {
        init(); // 初始化并查集
        for (int i = 0; i < n; i++) 
        { // 遍历所有的边
            if (same(edges[i][0], edges[i][1]))  // 构成有向环了，就是要删除的边
                return edges[i];
            join(edges[i][0], edges[i][1]);
        }
        return {};
    }

    // 删一条边之后判断是不是树
    bool isTreeAfterRemoveEdge(const vector<vector<int>>& edges, int deleteEdge) 
    {
        init(); // 初始化并查集
        for (int i = 0; i < n; i++) 
        {
            if (i == deleteEdge) 
                continue;
            if (same(edges[i][0], edges[i][1]))  // 构成有向环了，一定不是树
                return false;
            join(edges[i][0], edges[i][1]);
        }
        return true;
    }
public:

    vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) 
    {
        int inDegree[N] = {0}; // 记录节点入度
        n = edges.size(); // 边的数量
        for (int i = 0; i < n; i++) 
            inDegree[edges[i][1]]++; // 统计入度
        vector<int> vec; // 记录入度为2的边（如果有的话就两条边）
        // 找入度为2的节点所对应的边，注意要倒叙，因为优先返回最后出现在二维数组中的答案
        for (int i = n - 1; i >= 0; i--) 
            if (inDegree[edges[i][1]] == 2)
                vec.push_back(i);
        // 处理图中情况1 和 情况2
        // 如果有入度为2的节点，那么一定是两条边里删一个，看删哪个可以构成树
        if (vec.size() > 0) 
        {
            if (isTreeAfterRemoveEdge(edges, vec[0])) 
                return edges[vec[0]];
            else
                return edges[vec[1]];
        }
        // 处理图中情况3
        // 明确没有入度为2的情况，那么一定有有向环，找到构成环的边返回就可以了
        return getRemoveEdge(edges);
    }
};

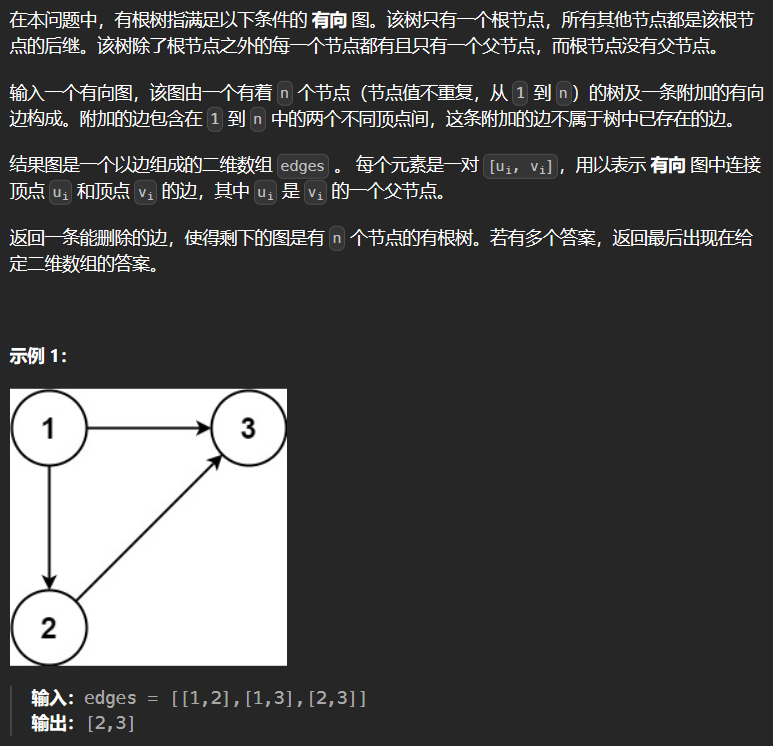
12. 模拟

12.1 657-机器人能否返回原点

657

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
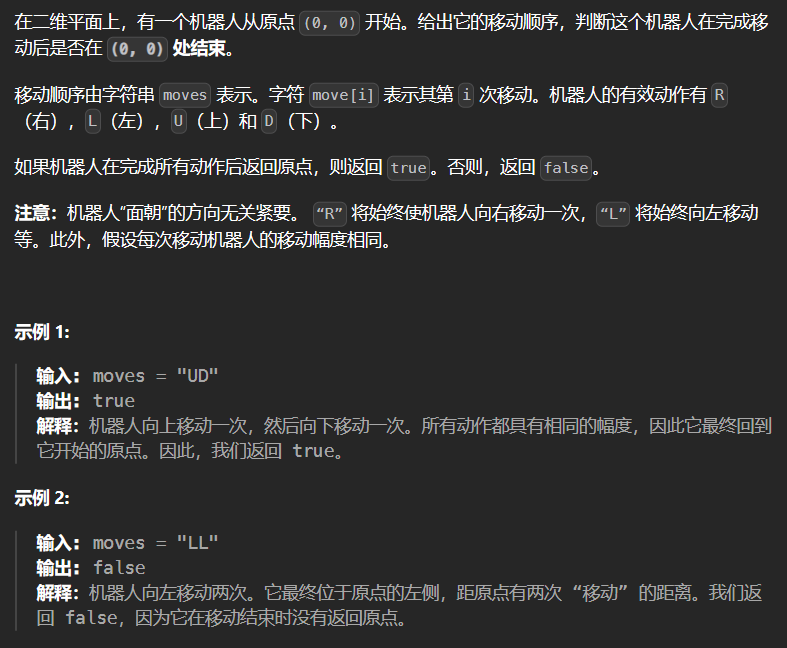
class Solution {
public:
    bool judgeCircle(string moves) {
        int x = 0, y = 0;
        for (int i = 0; i < moves.size(); i++) 
        {
            if (moves[i] == 'U') y++;
            if (moves[i] == 'D') y--;
            if (moves[i] == 'L') x--;
            if (moves[i] == 'R') x++;
        }
        if (x == 0 && y == 0) 
            return true;
        return false;
    }
};

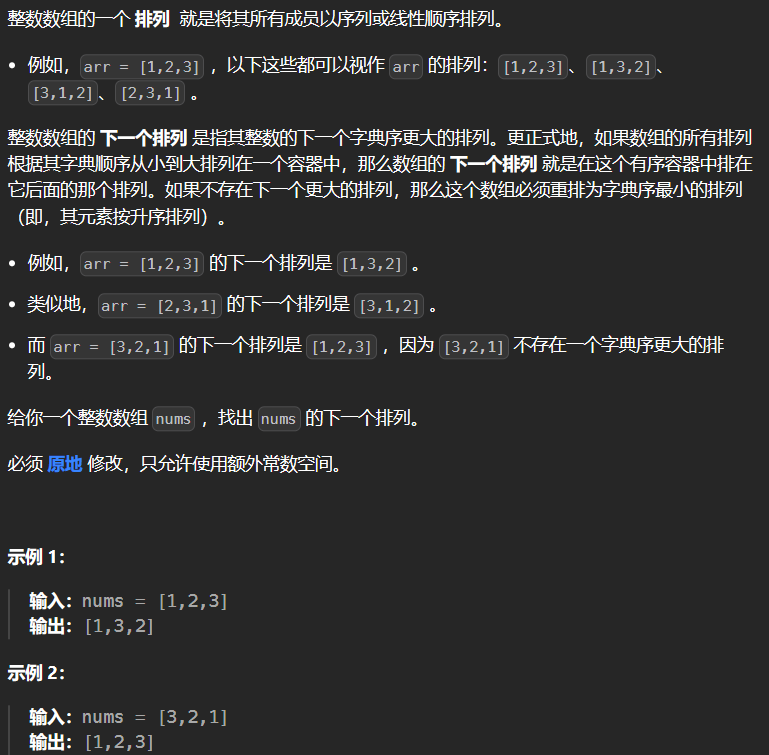
12.2 31-下一个排列

31

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    void nextPermutation(vector<int>& nums) {
        for (int i = nums.size() - 1; i >= 0; i--) 
        {
            for (int j = nums.size() - 1; j > i; j--) 
            {
                if (nums[j] > nums[i]) 
                {
                    swap(nums[j], nums[i]);
                    sort(nums.begin() + i + 1, nums.end());
                    return;
                }
            }
        }
        // 到这里了说明整个数组都是倒叙了，反转一下便可
        reverse(nums.begin(), nums.end());
    }
};

13. 位运算

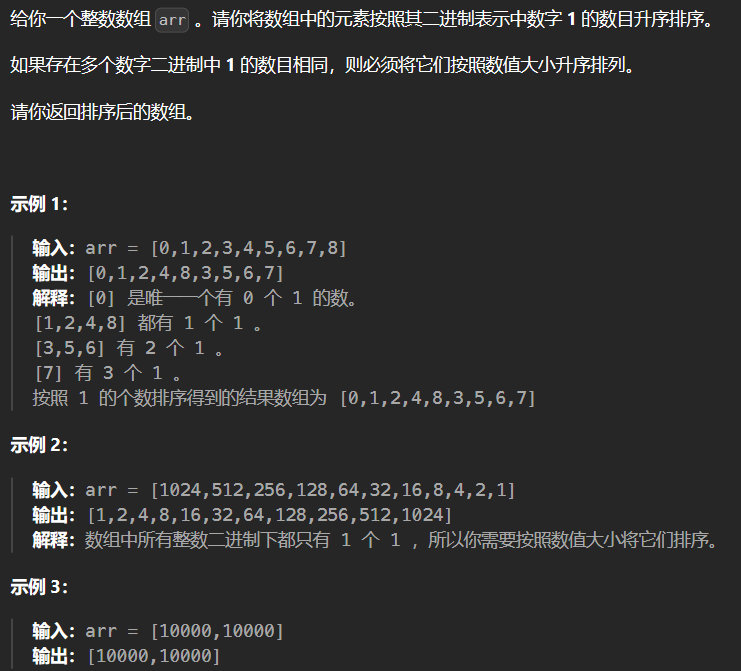
13.1 1356-根据数字二进制下1的数目排序

1356

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
private:
    static int bitCount(int n) // 计算n的二进制中1的数量
    { 
        int count = 0;
        while(n) 
        {
            n &= (n -1); // 清除最低位的1
            count++;
        }
        return count;
    }
    static bool cmp(int a, int b) 
    {
        int bitA = bitCount(a);
        int bitB = bitCount(b);
        if (bitA == bitB) 
            return a < b; // 如果bit中1数量相同，比较数值大小
        return bitA < bitB; // 否则比较bit中1数量大小
    }
public:
    vector<int> sortByBits(vector<int>& arr) {
        sort(arr.begin(), arr.end(), cmp);
        return arr;
    }
};