1. 整形在内存中的存储和整形提升

整数在内存中存储的是补码

那为什么在内存中偏要存储补码呢?

比如 (1-1)

这里我们要解释

补码可以将符号位和数值域统一处理
同时加法和减法也可以统一处理 (CPU只有加法处理器)
还有 补码和原码,原码和补码转化的方式是一样的(都是取反+1),不需要额外的电路

因此在内存中存储补码可以方便运算

简述一下整形提升

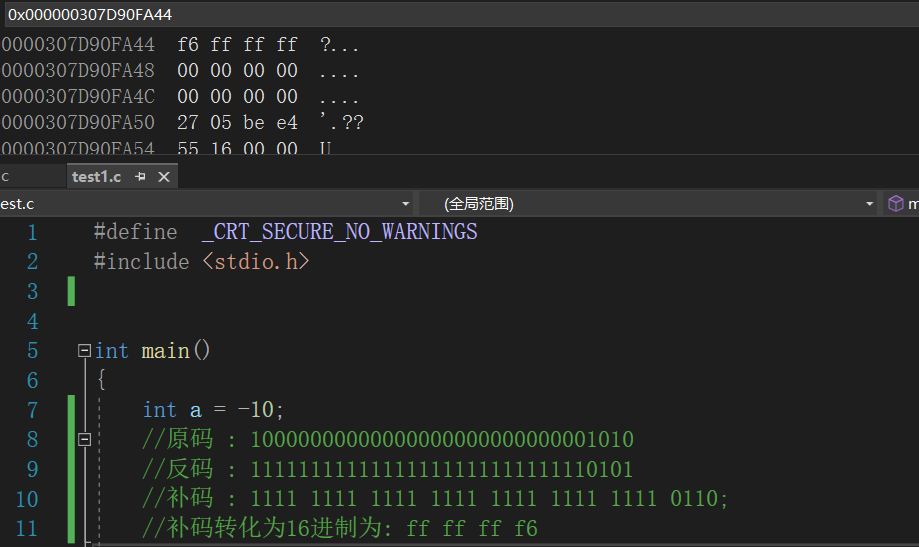
一、

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
//-1 的补码为
//11111111111111111111111111111111

char a = -1;
//因为 a 为 char 类型,所以只能存一个字节(8bit) 即为
//11111111

//又因为打印的方式为 %d 即为整形方式打印 所以要整形提升
//(因为为有符号类型,所以前面补1) 即为
// 11111111111111111111111111111111 (补码)
//转换为原码则为 10000000000000000000000000000001 (即为-1)


signed char b = -1;

//b为有符号字符类型,计算方式与a相同

unsigned char c = -1;
//11111111(存储内容)
//因为为无符号类型,且需要整形提升 所以前面补0 即为
//00000000000000000000000011111111

//因为其为无符号类型 所以原反补码相同
//即不需要转化.直接打印出来
//即为255
printf("%d %d %d",a,b,c); //-1 -1 255

有符号位的整形提升前面补1
无符号位的整形提升前面补0

二、

1
2
3
4
5
6
7
8
9
10
11
char a = -128;
//-128 的补码为 11111111111111111111111110000000
//所以在a中存储的为后8bit位即为
//10000000
//又因为要以无符号整形打印 所以要整形提升,又因为char为有符号类型所以补1
//11111111111111111111111110000000

//又因为数据要以 %u解读 即为无符号类型,即原反补相同,所以直接打印
//即为4294967168

printf("%u",a); //4294967168

char默认为 signed char 还是 unsigned char 并没有标准规定,取决于编译器
但 int 默认为 signed int
short 默认为 signed short

2. 大小端存储的介绍

在整形存储方式中我们注意到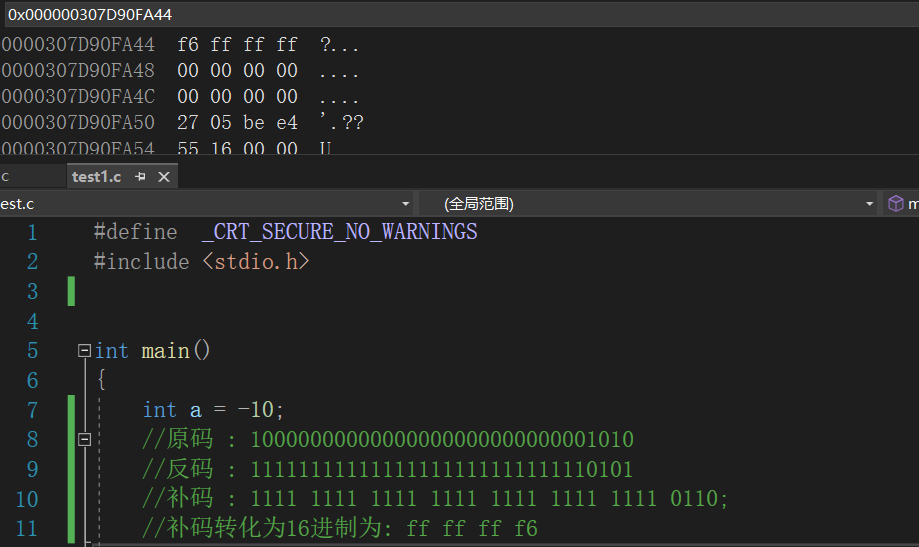

我们运算出的 内存存储数据 在内存是反着来的

大小字节端的内存处理方式

大端存储模式(大端字节序) : 数据的低位字节序保存在内存的高地址处,数据的高位字节序保存在内存的低地址处
.
小端存储模式(小端字节序) : 数据的高位字节序保存在内存的高地址处,数据的低位字节序保存在内存的低地址处

什么是低位字节序和高位字节序呢

我们举一个很简单的例子

1
int a = 0x11223344;

就以这个a为例子

在a中, 11 就是最高位字节序,44就为最低位字节序

写出一个程序,判断当前机器的字节序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int main()
{ 
  int a = 1; 
  //可以知道 a 的16进制补码为 00 00 00 01
  
  char *p = (char*) &a; 
  //取出a的地址并强制转换为char* 并将地址交付给 p
  //从而转换为存储a最低地址的一个字节即 01 或 00 
  
  //再进行判断
  if (*p == 1)
  {
    printf("小端"); //即低字节序存储在低地址处
  }
  else if(*p == 0)
  {
    printf("大端"); //即高字节序存储在低地址处
  }
}

3. 浮点型在内存中的存储

浮点数的存储为IEE 754规定,任意一个浮点数可以表示为下面的形式:

(-1) ^S * M * 2 ^E
(-1) ^S 表示符号位, S == 0为正 , S == 1为负
M表示有效数字, 1 <= M < 2
2^E表示指数位

1
2
3
浮点数: 5.5 (十进制)
二进制: 101.1 --> 1.011 * 2^2 --> (-1)^0 * 1.011 * 2^2
                                S == 0   M = 1.011  E = 2

每个值该分配多少空间,IEE 754 也有规定

float:


.
.
.

double:

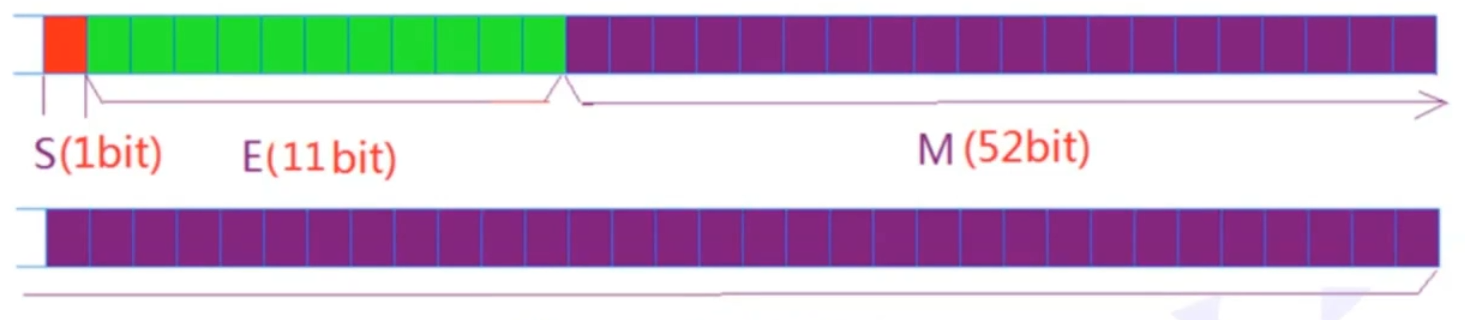
关于M:
前面提到了M总是为1-2之间,因此M的表达式总是为
1.xxxxxxx
所以为了拥有更大的存储上限,IEE规定这个1可以省去
M内只存入小数点后几位

关于指数E:
首先,E是一个无符号整数
所以E为8位时,其取值范围为 0255
E为11位时,其取值范围为 02047

但是我们都知道指数在科学计数法中是可以为负数的
所以规定

存入内存时E的真实值必须加入一个中间数
8位时这个中间数为127
11位时这个中间数为1023

指数存入就是以上这些
指数取出就又可以分为三种情况了

情况 处理方式
E不为全0并且不为全1 对指数减去127得到真实值,再将有效数字M前加上一位1
E为全0 此时E的真实值即为 1-127 或 1-1023,有效数字M前不再加1,而是还原为 0.xxxxx的小数,这样做表示±0,以及接近于0的很小数字
E为全1 表示±无穷大(正负取决于S)

内存中怎么装这些东西?

1
2
3
4
5
6
7
8
9
10
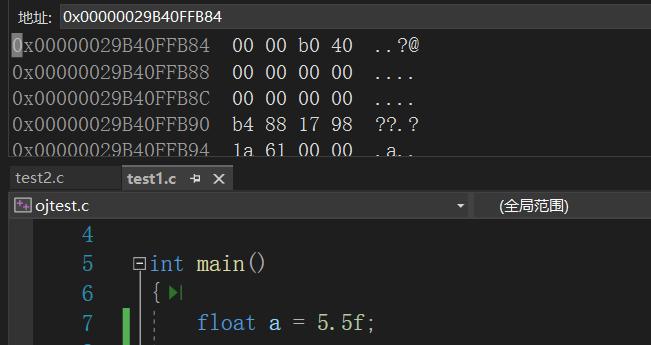
11
float a = 5.5f;
//转化为二进制为 101.1

// (-1) ^0 * 1.011 * 2 ^2
// s === 0  M===011  E=2+127

// 0 10000001 01100000000000000000000
// 01000000101100000000000000000000
// 0100 0000 1011 0000 0000 0000 0000 0000
// 40 b0 00 00
// 以上十六进制数列即为内存中存放的数据

我们可以验证一下